同调代数

　　代数学的一个非常重要的分支，是由美国的数学家与欧洲的数学家在20世纪40年代彼此独立而几乎同时开始发展起来的。同调代数源出于代数拓扑学，因而它仍保留着一些代数拓扑学中所用的术语，如循环（闲链）、边缘（边缘链）等等，而代数拓扑学本来就是把几何概念转换成代数概念的一种理论。
　　代数拓扑学中的同调群概念与同调代数有密切联系。在n维欧氏空间En中适当取q+1个点α0,α1,…,αq，q≤n，它们将张成一个q维超平面。取，则所有这些x之集成为一个q维单形Sq,常记为(α0,α1,…,αq)。它以αi为其顶点,αi全为正数的点称为内点,其余的点,称为边缘点。称为其一个边缘面,是一个r维面，这里i0,i1,…,ir是0,1,…,q中的任何r+1个数,取C为En中有限个单形之集,其中任两个单形之交或为空集,或为它们的一个r维面，而且若Sq属于C,则其任一个r维面也必属于C。以Cq表示由C中所用的q维单形Sq所生成的加法自由交换群，并于Sq=(α0,α1,…,αq)时，定义

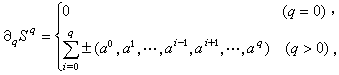
这里的±号是按照某种定向规则而确定的，于是得到一个链复形

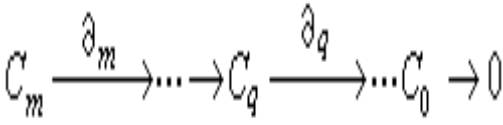,　　　(1)

且嬠q-1嬠q=0，所以Im嬠q吇Ker嬠q-1（Im嬠是嬠的像,Ker嬠是嬠的核）,这时,商群Hq=Ker嬠q/Im嬠q+1称为C的第q个同调群，同调群的理论集中地反映出复形的有关其边缘的几何性质。“同调”一词源出希腊文,意指“和谐”或“一致”。
　　代数学家不考虑上述同调理论中的几何意义，直接讨论式(1)，研究其同调群,式中的Ci已不仅是一些交换群,而是环上的模。同调代数的理论已经变成研究环、一般代数、李代数与群的一种不可缺少的有力工具。　
　　以下述及的环U与B都有单位元，模都是酉模，且一般是左U模。左U模范畴记作。
　　复形与同调模 　范畴中的一个复形是一列(A,嬠)

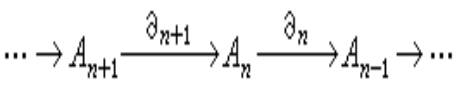,　　　(2)

式中An都是U模,嬠n是模同态,而且嬠n-1嬠n=0, Ker嬠n称为n循环,lm嬠n+1称为n边缘。于是Im嬠n+1吇Ker嬠n，定义是复形(A，嬠)的第n个同调模。若式(2)中对所有的n都有Im嬠n+1=Ker嬠n,即所有Hn(A,嬠)都等于0，则(A,嬠)是一个正合列。特别,若在n≥3与n<0时，所有的 An都等于 0，而(2)又正合，则为短正合列,这时嬠2必为单同态,嬠1必为满同态，而A0=A1/嬠2A2。
　　假定(B,d)也是一个复形, 设有模同态?n:An→Bn,使下图可交换

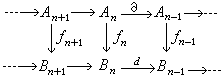
则?={?n}称为由(A,嬠)到(B,d)的一个复形映射。于是,以所有的U模的复形为对象,以复形映射为态射,则得一个阿贝尔范畴,称为复形范畴,记为Ucm。由于,所以,?n将引出Hn(A,嬠)到Hn(B,d)的一个模同态?n,称为同调映射。若?与g都是(A,嬠)到(B,d)的复形映射，且有，使对所有的n，恒有,则?与g为同伦的，记为h:?埍g，这时必有?n=gn。
　　固定任一整数n,每一个复形(A,嬠)将对应其第n个同调模Hn(A,嬠),而复形映射?:(A,嬠→(B,d)将引出同调映射?n, 因此Hn是一个由Ucm到的函子,它把(A, 嬠)变成Hn(A,嬠),把?:(A,嬠)→(B,d)变成?n，这个Hn称为第n个同调函子。
　　复形的短正合列 是指如下的交换图：

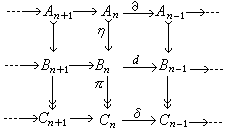　　　(3)

其中各行均为复形, 各列均为短正合列, 表单同态，表满同态。对于(3), 有在同调代数中各个方面都起着重要作用的同调正合列定理：
　　有连接映射(模同态) 使有正合列（δ，嬠，d 等记号都省掉）

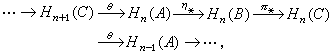
与上述同调相对偶的是上同调。设An为U模，则

　　　(4)

称为上复形,式中嬠n嬠n-1=0,而商模称为上复形(4)的第n个上同调模。
　　投射分解与内射分解 　正合列

,　　　(5)

当p0,p1,p2,…,pn,…都是投射模时,称为A的投射分解。由于每一个U模都是一个投射模的同态像，所以，每一个U模A都有投射分解。如果(5)中存在一个最小的n,使Im嬠n为投射模,那么,尽管A的投射分解并不惟一(可能有其他的投射分解)，这个n却是不变的,称为A的投射维数, 记为PdA=n。如果每一个lm嬠n都不投射,那么PdA=∞。于是,PdA=0的意思就是A为投射模；若PdA=1,则A可分解成两个投射模之商，A=p0/p1；若PdA=2,则A是三个投射模之商，A=p0/p1/p2,…。 范畴中各模的最大投射维数是这个范畴的一个总体性质，因而也是环U本身的一个总体性质，所以称为U的左总体维数。已知:若ldU=0,则U为满足极小条件的半单环;若ldU=1,则U为左遗传环。同样可定义U的右总体维数rdU。一般说来，U的左、右总体维数并不相等。
　　与上述投射分解相对偶，正合列

，

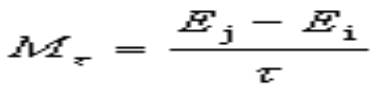当I0,I1,…都是内射模时，称为A的内射分解。由于每一个A都可嵌入到一个内射模内，所以A的内射分解一定存在。同样可定义A 的内射维数IdA。在中各模的最大内射维数正好等于U的左总体维数ldU。
　　导函子 　设T是一个自 到BM 的共变加法函子,由下列的办法来定义的一系列新的函子LnT与RnT，称为由T 所导出的导函子。
　　取A与B均为U模，?:A→B为模同态,(p,嬠)与(Q,d)分别为A与B的投射分解，则有复形映射{?n}使有交换图

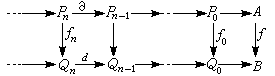
于是有交换图

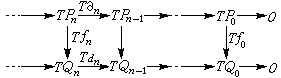(6)

这里两行都是B模的复形，它们的第 n个同调模，将表以与， 而由T?n所引出的同调映射则表以LnT(?),其实这些LnTA与LnTB并不随所取的投射分解而变，换成A与B的其他的投射分解，仍得到同样的LnTA与LnTB。同时,LnT(?)也不随所取的复形映射{?n}而变,换?n为gn,只要图(6)仍然是可交换的，那么就有相同的同调映射。 因此,由A变成LnTA，由?:A→B得到LnT(?)，则得一个共变函子LnT，称为T的左导函子。
　　若改用A的内射分解，则用同样的方法可得到T的右导出函子RnT，它是一个共变函子。
　　如果 F是一个逆变加法函子，那么取 A的投射分解(p,嬠)，就得上复形(Fp，F嬠),其第n个上同调模将记为RnF(A)，因而可由F导出的右导出函子RnF,它是一个逆变函子。
　　若对所有的n>0恒有LnTA＝0，则A称为一个左T-零调模。零调模在谱序列的理论中非常重要。
函子圱与Tor 　取M为右U模,对任一个左U模,定义,并对模同态σ:A→B,令T(σ)=1圱σ:M圱A→M圱B, 则得一个由到交换群范畴AG的共变加法函子T,此T也常表成M圱-。由T所导出的第n个左导出函子将表以Tor將(M,-)，换言之,若取A的一个投射分解为(p,嬠),则得一个复形(M圱p,1圱嬠)，此复形的第n个同调模就是Torn(M,A)(U有时可省去)。特别，Tor0(M,A)=M圱A。
　　同样，让A固定，则得函子－圱A，由其导出的第n个导出函子为Torn(-,A)，所以Torn(-,-)实际上是一种双函子，它对两个变量（让其一固定，另一个变动）都是共变加法函子。
　　符号Tor是英文Torsion一字的前三个字母，它的意思是“挠性质”。假定U是一个整环（无零因子的交换环）,而A是一个U模，让tA={α∈A│有某一非零α∈U，使αα=0},于是tA是A的一个子模,称为A的挠子模。让A对应tA即得 到其自身的一个共变函子t；另一方面,让Q为U的商域（也看成U模）,令M=Q/U为商模，则可证明，函子t（可称为挠函子）与函子Tor(M,－)是自然等价的，故用符号Tor。
　　函子Hom与Ext 　固定一个左U模x，对于任一个左U模A，定义 FA=HomU(A,x)，并对?:A→B，定义F(?)：Hom(B,x)→Hom(A,x),使在σ∈Hom(B,x)时有交换图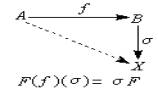(7)。

(7)

F(?)(σ)=σF,于是,F是一个由 到AG的逆变函子，其第n个右导出函子RnF将表以Ext(-,x)。因此,先取A的任一个投射分解(ρ,嬠)，再作上复形, 则其第n个上同调模就是 Extn(A,x)，特别，Ext0(A,x)=Hom(A,x)。
　　如果让A固定，令TX=Hom(A，x)，并对g:x→Y,定义T(g):Hom(A,x)→Hom(A,Y),使T(g)(τ)=gτ如交换图(8)，则T为到AG的共变函子, 其第n个右导出函子将表以Extn(A,-)，换言之，Extn(-,-)是一个双函子，它对第一个变量A是逆变的（让x 固定时）；而对第二个变量x是共变的（让A固定）。

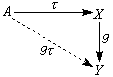(8)

　　与Tor的情况类似，Ext是英文 Extension一字的前三个字母组成的符号，其意为“扩张”。设x与A都是U模，E称为x由A的一个模扩张，是指有短正合列0→x→E→A→0。两个扩张E与E┡称为等价的,意指有φ:E→E┡使下图可交换

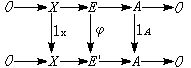
这里的φ必是一个模同构,因而上述等价性是一种等价关系，以e(x,A)表所有等价类之集合，可以证明，e(x,A)与Ext1(A，x)是一一对应的。所以可认定e(x，A)就是Ext1(A,x)。
　　群的同调与上同调 　设G为乘法群，Z表整数环，以G的所有的元素为生成元素可得一个加法自由群ZG,因此ZG 中每一个元素都惟一地表成 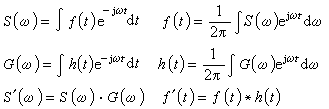的形状，这里m(x)∈Z，且只能有有限个m(x)不为0,再定义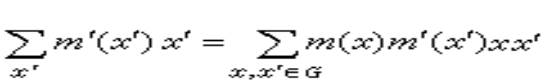，则 ZG是一个环,称为Z上的群环。任一个ZG模也称为G模。如果在z∈Z时,定义，则Z作成一个左G模。
　　当A为G模时， 称为G的其系数在A内的上同调群。对偶地,若B为右G模,称为G 的其系数都在B内的同调群。不难证明

这里的称为ZG的增广理想，它在群的同调理论中十分重要。
　　各种群的 Hn与Hn的计算与理论是同调代数与群论中的重要研究课题。
　　谱序列 　它是同调代数中的一个重要的理论，也是一种研究同调模的重要方法。
　　设A是一个U模,若有模自同态d:A→A使B=Imd吇Z=Ker d,即dd=0,则(A,d)称为一个微分模,d是其微分,而商模Z/B是(A，d)的同调模H(A,d)。与复形的情况类似，B为d的边缘,而Z为d的循环。微分模的序列{Ar,dr}(r≥1 是整数)称为一个谱序列，是指对每一个r都有。让Z2Ker d1,B2=Im d1,则A2=Z2/B2,又定义Z3与B3,使A3=Kerd2/Imd2=(Z3/B2)/(B3/B2)=Z3/B3,…,依此类推,可让Ar=Zr/Br,于是得一链，令,,则A∞=Z∞/B∞称为谱序列{Ar,dr}的极限模。在r很大时，Ar可作为极限模的“近似”。
　　在同调代数中常用到的谱序列实际上是由双分次模所组成的，所谓双分次模，就是一些模Epq的集合，p与q都是整数。设E与D都是双分次模,且有整数对(α,b)),使对任何p、q都有一个模同态，则d:E→D称为具有双分次(α,b))的映射。若d:E→E有次数(α,b)),且dd=0，即,凬p,q，则d是微分，而为其同调双分次模。假定(Er,dr)都是微分双分次模,且,那么，这对于(Er,dr)也是一个谱序列。
　　用过滤的办法,可以从一个复形(A,嬠)得到一个很有用处的谱序列。假定对每一个p∈Z，FpA都是A的一个子复形，并且有

,

则F称为复形(A,嬠)的一个过滤。于是,对任何p就有一个复形的短正合列，由同调正合列定理，得

, (9)

让

,

式(9)就可改写为

,

这里α，β，γ是有次数(1，-1)，(0,0)与(-1，0)的映射。以E1表示双分次模{Epq},并取，易知，d1:E→E有次数(-1,0),且d1d1=0,故d1是E1的微分。以E2表其同调双分次模，再适当定义d2:E2→E2为E2的微分。依此类推,即得一个谱序列(Er,dr),只要F取得恰当，这个谱序列可以提供(A,嬠)的同调模的一些信息。