第零章          矢量分析与绪论

【教学目的】通过本章教学，使学生了解矢量场与标量场的含义，掌握矢量场与标量场的散度、旋度、梯度等三种运算方法。

【重点难点】

矢量场的散度、旋度运算及标量场梯度的运算。

 

§0.1   矢量分析

1．矢量代数

（1）   三矢量混合积运算

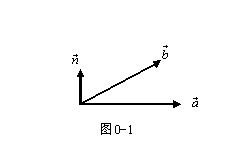矢量点乘：

矢量差乘:

矢量混合积

:

（2）   三矢量的矢积运算

 

2．散度、旋度和梯度

（1） 矢量场的散度

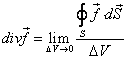
（2） 矢量场的旋度

 

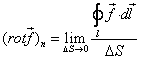
（3）   标量场的梯度

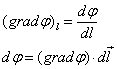
（4）   积分变换式

高斯定理：

斯托克斯定理：

（5）   直角坐标系中散度、旋度和梯度公式

设

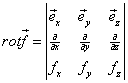
（6）   算符

在直角坐标系中

 

算符的特点：既具有矢量性又具有微分性。

散度、旋度和梯度可用算符来表示。

高斯定理：

斯托克斯定理：

3．关于散度和旋度的一些定理

 （1）

 （2）

 （3）若，则

 （4）若，则

4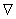．算符运用公式

常用公式如下

作为一个例子，证明

 

证：利用的微分性，有

注意表示作用在上的微分。

再利用的矢量性，有

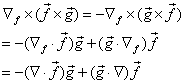
同理有

 

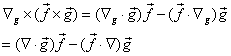
于是

5．曲线正交坐标系

（1）圆柱坐标系

（2）球坐标系

6．并矢和张量

（1）并矢

   

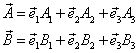
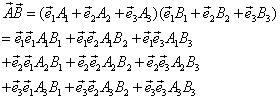
并矢共有9个分量。显然

（2）二阶张量

两矢量的并矢又称为二阶张量，写成

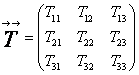
   单位张量

（3）张量的代数运算

 

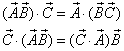
显然有

注意：二阶张量与矢量的点乘为一矢量。

并矢与另一并矢的双点乘定义为

（4）张量分析

（）