【教学目的】

通过本章教学，使学生了解描述电磁场的基本规律，电磁场与物质相互作用时的极化与磁化现象，电磁场的边值关系以及电磁场的能量与能流。

【重点难点】麦克斯韦方程，电磁场的边值关系，电磁场能量守恒定律。

第一章  电磁现象的普遍规律

§1.1   电荷和电场

1．库仑定律

（1）         库仑定律

两点电荷之间的相互作用力为

    （库仑定律）

式中为真空介电常数，＝8.85 （SI制）

 

（2） 作用力的本质

（a）超距作用，。

（b）电场传递，

在静电情况下，两种描述情况等价。

在时变情况下，后一种观点是正确的。

（3）点电荷产生的电场

多个电荷产生的电场

      （场的矢量叠加）

 

 

 

 

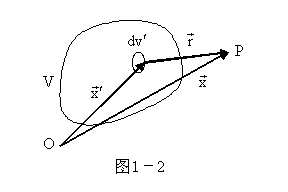（4）连接分布电荷所产生的电场

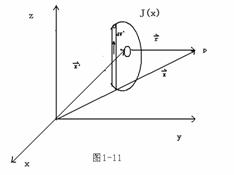
如图1-2所示，连接分布电荷所产生的电场为

式中； ，。

2．高斯定律和电场的散度

（1）   高斯定律

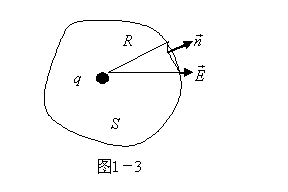如图1-3所示，作一曲面包围点电荷，点电荷的电场在封闭曲面上的积分，总通量为

     （高斯定理）

下面对高斯定理进行证明。

 

 

 

[预备知识]立体角概念

如图1-4所示，针对视点O的微分立体角定义为

若视点O在闭合面内，则有

若视点O在闭合面外，则有

高斯定律的证明

证：

,,

  证毕。

若闭合曲面内有多个点电荷，则高斯定律的形式是

  

若电荷连续分布，其密度为，则有

  

V为S所围的体积。

此式也为高斯定律的积分形式。

注意1：闭合曲面外的点电荷对总通量无贡献，并不意味着对电场无贡献。

注意2：若已知电场的有关对称性质，则可用此定理求空间某处的电场。

（2）   高斯定律的微分形式

表示散度

物理意义：

（a）电力线的发散性或会聚性；

（b）高斯定律比库仑定律更具有普遍性。库仑定律仅适用静电场，而高斯定律还可适用时变电场；

（c）电场具有局域性。

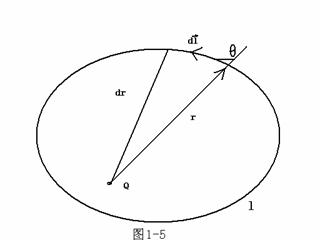
3．静电场的旋度

可以证明，静电场沿任意闭合回路的积分总为零，即

证明：

考虑一个点电荷产生的电场

                                                     
　

注意：对于任何静电场均成立

的微分形式为

物理意义：静电场的电力线并不闭合

可用反证明法证明。

4．举例

例1：电荷Q均匀分布于半径为a球体内，求各点的电场的旋度，并由此直接计算电场的散度。

解：[分析]由于电荷分布是球面对称的，故其长也是球形对称的，。

即电场仅与观察点与球心的距离有关，

与其方位无关。可以分两种情形讨论：

（1）    情形

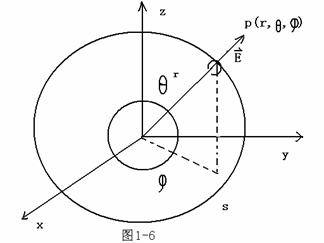
 采用球坐标系，如图1-6所示，作一球面，

其上P点坐标，由高斯定理

，

矢量形式为

（2）情形

在球内做一高斯球面，球面所围电量为

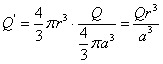
应用了高斯定理，得

。

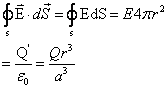
现在计算场的散度 ：

（a）情形

      (r0) [在直角坐标系中，证明略]

（b）情形

作业：P45， 2，3，4。

§1.2   电流和磁场

1．电荷守恒定律

（1）电流密度

电流密度定义为其大小可以定义为垂直穿过单位面积的电流强度。在均匀分布情况下，电流密度为

 

方向为电流方向。

（2）电流强度与电流密度的关系

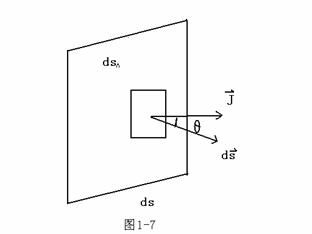穿过面元的电流强度为

通过任意闭合曲面S电流为

对于闭合面则有

。

（3）在离散情况下的电流密度

如图1-8所示，假定电流密度为，平均速度为，

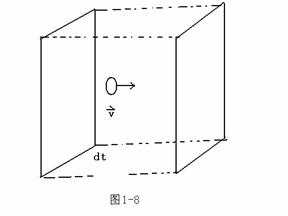
写成矢量形式，则为

(4) 电荷守恒定律

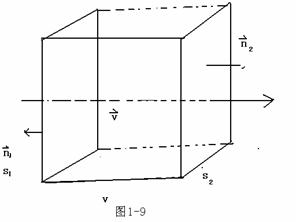
如图1-9所示，流进V中的电量为

V中单位时间电荷增加量为

由于电荷守恒，故有

此式即为电荷守恒定律。利用数学上的高斯定理，可得

   （微分形式 ）

对于恒定电流，因，故有

 

2．毕奥－萨伐尔定律

（1）安培力

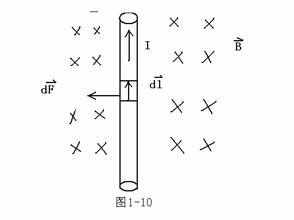
如图1-10所示，考虑磁场中电流受到的力

＝

为处的 磁感应强度，此力称为安培力。

（2）毕奥－萨伐尔定律

，

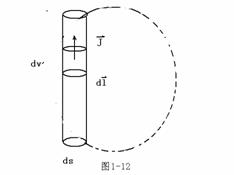
对于细导线产生的磁场，如图1-12所示，则有

[注：为垂直与方向上的投影，与方向相同]

 

 

 

 

 

 

 

3．磁场的环量和旋度

（1）安培环路定律

考虑无限长细导线电流产生的磁场，如图1-13所示。安培环路定律表述为

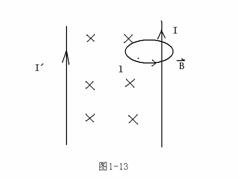
其中I为环路所围曲面的总电流。

即的环流为。

以无限长直流导线产生磁场为例，给以证明如下：

  

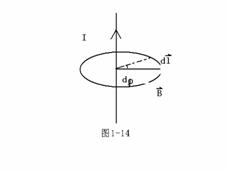
方向与方向相同。

又因为

所以

证毕。

注意1：安培环路定律对任意闭合回路均成立；

注意2：所围电流可正可负，（带数量）。其正负可由右手确定（拇指为电流正方向，回路的方向与四指方向有关系）。

注意3：利用安培环路定律可求具有特定对称性的磁场。

注意4：回路外所产生的磁场其环流为零。即，但不代表对回路上的磁场无贡献。

注意5：仅对稳恒电流成立。

（2）安培环路定律的微分和积分形式

微分形式：

积分形式：

4．磁场的散度

由于是无源场，磁力线总是封闭的，所以有：

或.

注意：，对时变电磁场也成立。

讨论：若有磁单极子，则

5．磁场旋度和散度公式的证明

（1）的证明

又

＝

式中  [又称为矢势]

又

（2）的证明

利用公式

先求

  

利用公式

  

对于恒定电流，有

由于体积分包含所有电流，故有

（因）

所以

再计算

由于

，，所以

 

证毕

6.举例

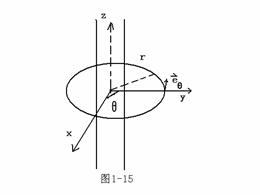电流I均匀分布于半径为a的无穷长直导线内，球空间个点的磁场强度，并由此计算磁场的旋度。

解：[分析]：在柱坐标系下研究，磁场具有轴向对称性，即，故可用安培环路定律求磁场。分两种情形讨论。

（1）    当时

 

 

应用安培环路定律，得

，

若计及方向，则

（2）    当时

电流密度（为均匀分布），作回路如图1-16所示。

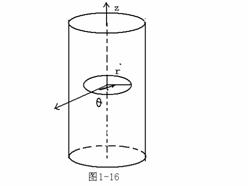
再求的旋度

（1）          当时，

 

（2）          当时，

§1.3   麦克斯韦方程组

1．电磁感应定律

（1）          电磁感应定律（1831年，Farady）

闭合线圈中的感应电动势欲通过该线圈内部的磁通量变化律成正比，其方向有楞次定律决定。磁通量

，［注：S为以为边界的任一曲面］。

楞次定律：感应电流所产生的磁场阻碍磁通的变化。

，

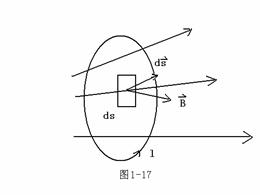
注：感应电动势方向由右手定则决定。

（2）电磁感应定律的积分和微分形式

由于感应电场的回路积分为电动势，故电磁感应定律可表示成下列的积分形式

式中为感应电场

应用斯托克斯定律，得微分形式

。

（3）          几点注意：

注意1：积分形式的回路可以是虚构的，也可以是导体（真实地），对于真实导体回路，则形成传导电流。

注意2：感应电场与静电场不同，起旋度不为零，或者说电力线是闭合的。

注意3：变化的磁场可以产生电场。

2．位移电流

（1）         问题的产生

对于恒定电流，有：

对于非恒定电流，有

例如，考虑电容的冲放电，如图1-18所示。电容器充放电，极板上的电荷随时间变化，故有。

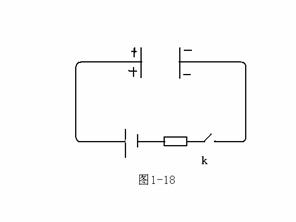另一方面，根据安培环路定律，有

这与电荷守恒定律发生矛盾，矛盾的根源在于，

安培环路定律是根据恒定电流测出的定律，即在

证明中运用了稳恒的条件。

（2）矛盾的解决——位移电流的提出

假定存在一个位移电流，使得

且假定位移电流也有磁效应，即

为了使与电荷守恒定律无矛盾，即，要求

又因为

所以

（3）真空中时变情形下的安培环路定律

安培环路定律：

注意1：位移电流为非真实电流，但有磁效应。

住意2：位移电流有变化的电场产生。

注意3：变化的电场产生磁场。

3．真空中的麦克斯韦方程组

综上所述，我们得到真空中麦克斯韦方程组

。

 

上述方程描述了电荷电流激发电磁场及其电磁场内部的运动规律。在无源区域，即，电磁场相互激发，会形成电磁波。

4．洛伦兹力

如图1-19所示，考虑带电体在，中所受力。

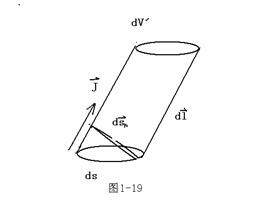电场力 

；

磁场力（安培力）

洛伦兹力

洛伦兹力密度

对于带电粒子e在，中受力，则为

§1.4   介质的电磁性质

1．关于介质的概念

介质有分子组成，可看成一个带电粒子的系统。

介质在电场中将产生极化现象，会出现束缚电荷。

介质在磁场场中将产生磁化现象，会出现磁化电流。

2．介质的极化

（1）   介质极化的定义

介质在外电场作用下，能产生宏观电偶极矩的现象。这样的介质，称为电介质（简称介质），通常为绝缘体。

（2）   电介质的分类

（I）介质分子无电偶极矩，即分子的正负电重心重合。

（II）介质分子有电偶极矩，但各分子的电偶极矩取向无规则，无宏观电偶极矩。

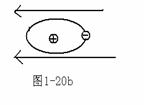
（3）   电介质在外电场作用下的极化

对于第I 类，各分子正负中心被拉开，如图1-20所示。

对于第II 类，各分子电偶极矩将有序化，如图1-21所示。

 

 

 

 

 

 

 

 

 

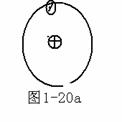
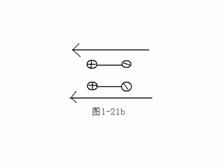
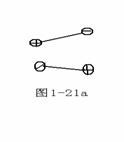
（4）   电极化强度矢量

介质在外场作用下，体积内总的电偶极矩（宏观电偶极矩）将不为零。

定义电极化强度矢量

，

n为单位体积内的分子数，为分子的的平均电偶极矩。

（5）   束缚电荷

由于极化，在某一体积内，将出现净余的正电荷或负电荷 称为束缚电荷，单位体积的束缚送电荷量称为束缚电荷密度。

（6）   电极化强度矢量与束缚电荷的关系

设每个分子的电偶极矩为，（相距为，电荷为q）,单位体积内的分子数目为n。极化后，各电偶极矩取向一致，如图1-22所示。

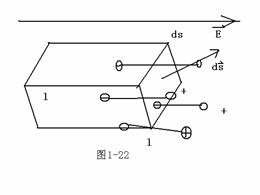
的方向与偶极矩不一定相同。穿出面的电荷量为

穿出任意的总电量为

根据前面的分析

。

束缚电荷还可出现在介质的分界面上，可定义面束缚电荷。

考虑两介质分界面的薄层，如图1-23所示。穿出的束缚电荷为

而穿出的束缚电荷为

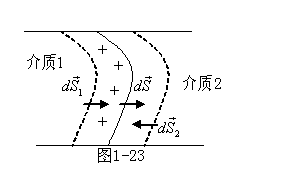注意到，薄层上的束缚电荷量为，

我们可得

令，可得

注意：（a）外均匀介质极化后介质内部一般都出现束缚电荷。

      （b）对于均匀介质，束缚电荷出现在自由电荷附近。

      （c）在两介质分界面上存在束缚电荷。

（7）电位移矢量与介质中的高斯定律

介质中的高斯定理

为自由电荷密度。

令

+

称为电位移矢量

于是有

 ―――－介质中的高斯定律

（8）介质的极化率

实验表明

＝

为介质中的电场，为介质的极化率。

，

3．介质的磁化

（1）基本原理

分子电流假设：每个分子提供一个微观分子电流，具有相应的分子磁矩，介质在屋外磁场时，其取向是无规则的，但在外场下则变为有序，这种现象称为磁化。

磁化现象的定义：

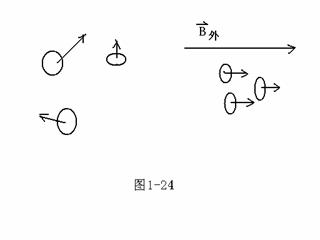介质在外磁场作用下产生宏观磁偶极矩。

介质磁化后，将产生磁化电流。

（2）磁化强度

 设每个分子磁矩为，平均磁偶极矩，

单位体积分子为数n,则磁化强度定义为

（3）磁化电流密度与磁化强度的关系

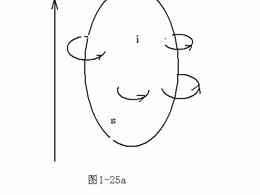设曲面的边界为，现研究一段边界，与交链的分子电流为

。

所以

又因为

，所以

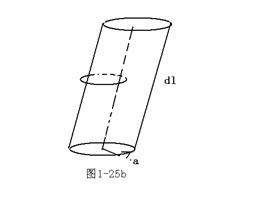
（4）极化电流

由于极化强度的变化，电偶极子振动形成的电流密度为

＝＝

（5）磁化强度与介质中安培环路定律

 

令———－称为磁场强度

则

—————称为介质中安培环路定律

（6）磁化率

试验表明：

＝

――――介质的磁化率，若为常数，称为线性介质。

，

，为相对磁导率。

4．介质中的麦克斯韦方程组

介质中的电磁场满足

其积分形式为

，

其中有

物质方程

＝，，。

作业：：5，6，7。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

§1.5   电磁场的边值关系

1．问题的提出

在外场中，在两种介质的边界面上会出现束缚电荷和束缚电流（极化电流），使两侧场量发生变跃变。例如：下面讨论场分量在边界面两侧的跃变。问题是在分界面上两侧的场量满足怎样的关系?

2．场的法向分量边值关系

（1）法向分量的跃变

 

 

因为

,

,。

所以

写成矢量形式为

推论：

（2）法向分量连续

利用，与上面同样的推导，可得

3．场的切法向分量边值关系

（1）表面电流分布

定义电流线密度为垂直穿过单位长度的电流强度

其方向为该点电流的方向。

如图所示，考虑电流分布在曲面上，穿过任意线段的电流为

为曲面的法向方向。

（2）的切向跃变

应用安培环路定律

因

，

又因

所以

把分解成，可得

因为，所以

两边同乘，得

又因为

，

所以得边指关系

上式也可写成

（3）的切向连续

同理有

。

电磁场边值关系总结如下：

 

4．举例

无穷大平行板电容器内有两层介质，极板上面电荷密度为，求电场和束缚电荷分布。

解: [分析]：由对称性可以知道电场垂直于平板的方向，如图所示：

由于存在介质，介质被自由电荷所极化。故介质中总电场在不同介质可能不同？即。

介质1与下极板分界面：

因为，，所以

介质2与上极板分界面：

因为，，所以

在介质1，2分界面：

因为，所以

，

又因为，，所以

（边界条件自动满足）

下面求束缚电荷密度

因为

，

所以

所以

在介质1与下极板分界面处：

 

在介质2与上极板分界处：

可验证：

 

 

 

 

§1.6   电磁场的能量和能流

1．场和电荷系统的能量守恒定律的一般形式

（1）场的能量密度

电磁场的能量密度定义为场在单位体积的能量，通常与空时坐标有关。

（2）场的能流密度

单位时间内垂直通过单位横截面的电磁场能量，方向为能流传输方向。

（3）电磁场的转化和守恒定律

电场力对电荷做功为

使得V中磁场能量的增加率

而流入V中的电磁场能量为

根据能量守恒，有

其微分形式

2．电磁场能量能量密度和能流密度表示式

又因为

所以

与能量守恒定律的微分形式比较，得

  

在线性介质中，

但此式结果有普遍性。

分两种情况讨论：

（1）真空中

  ，，所以

，

（2）在线性介质中

  ，，所以

，

3．电磁场能量传输

 

以一个例子加以说明，

例：同轴传输线内导线半径为a，外导线半径为b，两导线间为均匀绝缘介质，导线载有电流I，两导线间的电压为U。

（1）忽略导线电阻，计算介质中的能流和传输功率。

（2）计及内导线电导率，计算通过内导线表面进入导线内的能流，证明它等于导线的损耗功率。

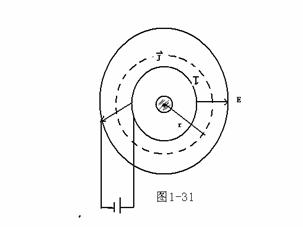解：设电荷线密度为

（1）

先求磁场，由安培定律得， ,

再求电场，由高斯定理得，

能流密度

再求传输功率，

先计算U和的关系，

，所以

传输功率：

这与电路中负载功率相似。

（2）

设内导线的电导率为，则根据欧姆定律

，所以，

这说明沿z方向也有电场，如图所示。

在内导线表面上，切向分量连续，

因此介质内表面电磁场强度

由上式可看出，为进入导体内的能流（－方向）。

进入内导体的功率为

作业。.8,9,11,12。

本章小结

1.      已知电荷电流求场

(1) 已知电荷分布，

(2) 已知电流分布，

，。

2.      静电场的特性

或

3.      高斯定理

 

或，

真空中

4．电荷守恒定律

，

稳恒时。

5.静磁场的安培环路定律

，

，

真空中。

6.静磁场的特点（下式可适用时变磁场）

7. 麦克斯韦方程组

＝+

，

真空中，

8.介质的极化

,

,

,

9.介质的磁化

，

＝，

，

。

10.边值关系

，。

，。

为从1指向2。

11.漏电介质中的传导电流

12.能量守恒定律

能流:，

磁场的能量密度，

电场能量密度。

能量守恒定律