【教学目的】

通过本章教学，使学生了解静电场的特点以及描述静电场的两个基本方程、电位函数的意义及其满足的方程、拉普拉斯方程的求解方法，掌握求解空间静电场问题的两个基本方法——分离变量法和镜像法。

【重点难点】

分离变量法和镜像法，电势的多级展开。

第二章  静电场

§2.1   静电场的标势及其微分方程

1．静电场的标势

（1）         描述静电场的基本方程

微分形式：，

积分形式: ,

由于静电场的无旋性，的线积分与路径无关。

因

所以

这说明了的线积分与路径无关，只与的值有关。

物理意义：

单位点电荷做功与路径无关。

（2）         电位函数

定义两点的电位差

利用电位函数可以求电场。

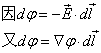
所以

电位函数的性质

（a）    电位函数仅具有相对意义，可以相差一个常数量；

（b）    对于有限的电荷体系，可令无限远处的电位为零（参考电位）；

任意点的电位为

（c）    电位是标量，且具有迭加性。

（3）   点电荷的电位函数

因点电荷的电场为

   故点电荷的电位为

    

（4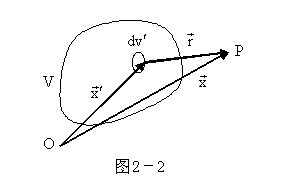）   多个点电荷的电位函数

（5）   连续分布电荷的电位函数

（6）   边值问题

如果在带电体附近有电介质或导体存在，则空间的电位函数的计算就比较复杂。因为，此时介质或导体中有束缚电荷或感应电荷存在，而它们的分布并不事先知道。解决这一问题的方法是求解满足边值条件的微分方程。

2．静电势的微分方程和边值关系

（1）   泊松方程

，

------------------称为泊松方程

称为拉普拉斯算符。

在无源区域，，有

-----------------称为拉普拉斯方程

（2）   电势满足的边值关系

出发点是电场的边值关系

               （1）

               （2）

利用上式，可以证明，两介质分界面上边值关系为

                   （3）

         （4）

证明：由（1）和（2）可以分别导出（3）和（4）。

（a）     这里直接给出一种证明（3）得方法。因为

所以

（b）

    

因，所以

（3）   静态时导体的一般性质和边值关系

（a）   导体内部不带电，电荷只分布在导体表面上；

（b）   导体内部电场为零；

（c）    导体表面上的电力线沿导体表面法线方向，导体为一等势体，其表面为等势面。

  根据以上特点，易得表面上电势满足

 

（4）   对于多层介质的静电场问题的一般解法

，

，

再加上边界条件。就构成静电场问题的边值解法。

3．静电场的能量

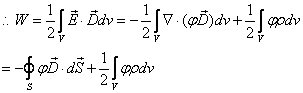
故当时，上式中的第一项为零。因此有

4．举例

例1：求均匀电场的电势，

解：如图所示，

由，得

 

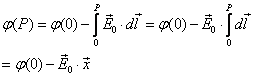
若取坐标原点的电势为零，则有

例2：均匀带电的无限长直导线的电荷线密度为，求电势。

解：[分析]这不是一个有限分布电荷产生电势的问题，因而求解较繁。 由于电荷分布具有轴对称性，故采用圆柱坐标系，如图所示。

利用公式

因电荷为线分布，，所以

又因，所以

选择一个参考点，使其电势为，则电势差为

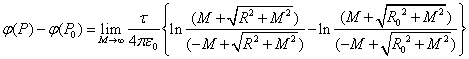
例3：求带电量Q，半径为的导体球的静电场的能量。

解：先求电势为

   

    导体球电势为

  

再根据公式，得静电场能量

§2.2   唯一性定理

静电问题归结为求解泊松方程，这需要边界条件，才能求得唯一解。问题是需要怎样的边界条件？

1．无导体存在时的唯一性定理

如图所示，考虑多层介质，在i,j区域的电势满足的方程和边值关系为

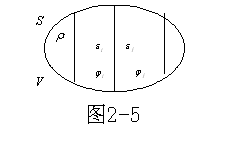
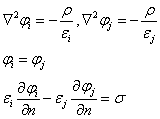
无导体存在时的唯一性定理

 设区域V内给定自由电荷分布，在V的边界上给定

（i）电势

（ii）电势的法向导数

则V内的电场就能唯一地确定。

证明：

设有两组不同的解满足定理中的条件

 

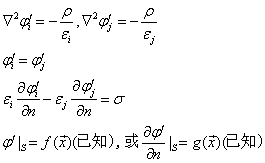
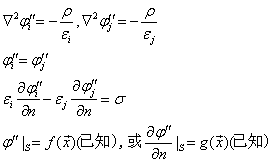
令，则有

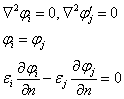
考虑第i个均匀区的界面上的积分

对所有分区域求和，得

（因）

因求和各项均为正，故有

因此。

2．有导体存在时的唯一性定理

有导体存在时的唯一性定理

 设区域V内有一些导体，给定导体之外自由电荷分布，给定导体上的电势或总电荷以及V的边界上的电势电势的法向导数，则V内的电场就能唯一地确定。

证明略

唯一性定理的意义

（1）        唯一性定理给出了确定静电场的条件，为求指明了方向。

（2）        更重要的是它具有十分重要的实用价值。

无论采用什么方法得到解，只要该解满足泊松方程和给定边界条件，则该解就是唯一的正确解。因此对于许多具有对称性的问题，我们可以不必用繁杂的数学去求解泊松方程，而是提出尝试解，只要满足方程和边界条件即为所求的解，若不满足，可以加以修改

3．应用举例

如图所示，两同心导体球壳之间充以两种电介质，左半部电容率为，右半部电容率为。蛇内导体球可带总电荷Q，外球壳接地，求电场和壳上的电荷分布。

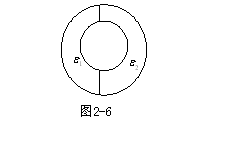解：设介质1，2的电场分别为，给出试探解，看是否满足边值关系，若满足，则根据唯一性定理，尝试解即为所求的解。

易验证满足边值关系

应用高斯定理，确定常数A。

再求

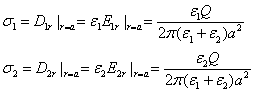
§2.3   拉普拉斯方程 分离变量法

1．拉普拉斯方程

若所求区域中的电荷密度，则其中的电势满足

---------------拉普拉斯方程

要求解此方程，需给出边界上电势满足的边界条件，若V中有多种介质，还需给出边值关系。

2．分离变量法

在分离变量法求解拉普拉斯方程时，通常根据边界的形状来选择适当的坐标系。

若边界形状为方形，则采用直角坐标系。

若边界形状为圆柱形，则采用圆柱坐标系。

若边界形状为球形，则采用球坐标系。

分离变量后，可将偏微分方程化为常微分方程。

3．球坐标系下拉普拉斯方程的通解

，

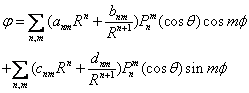
式中为待定常数，由边界条件确定之。为缔合勒让德函数。

 若电势具有轴对称性，即电势与方位角无关，则通解为

若电势具有球对称性，即电势与方位角无关，则通解为

4．应用举例

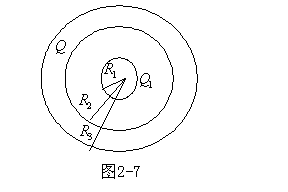
例1  一个内径和外经分别为的导体球壳，带电荷Q，同心地包围着一个半径为的导体球（），使这个导体球接地。求空间各点的电势和这个导体球的感应电荷。

解：设感应电荷为，在区域，电势为，在区域，电势为。注意到电荷只分布在导体表面上，故所求区域均无自由电荷，电势均满足拉普拉斯方程，且电势具有球对称性。因此，有

当，

当，

列边界条件：

因无穷远处的电势设为零

                     eq \o\ac(○,1)1

因内导体球接地

                     eq \o\ac(○,2)2

因球壳为等势面

                eq \o\ac(○,3)3

因球壳所带电量为Q

因为

所以

                  eq \o\ac(○,4)4

四个边界条件确定四个常数。将通解代入边界条件得

于是

感应电荷为

例2          电容率的介质球置于均匀外电场中，求电势。

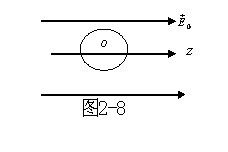解：[分析] 介质球将产生束缚电荷，如图所示。但电荷的分布未知，故求束缚电荷的场分布将是比较困难的，但可以通过边值问题反映出来。因边界形状为球型，故采用球坐标系。此问题有一个对称轴，即外电场的方向，电位与坐标无关。

设球外区域电势为，球内为，且满足

其通解为

列边界条件

在无穷远处有，故

        （1）

在时，电势应有限，故

（自然边界条件）    （2）

在介质球面上，有

                    （3）

                （4）

由（1）推出

由（2）推出

重写为

由（3）和（4）得

比较两边的系数，得

                         （5）

                        （6）

                        （7）

              （8）

联立（5）和（7），解得

联立（6）和（8），解得

于是

球内的电场为

 

介质的极化强度为

介质中总电偶极矩为

可以看出，的第二项就是由这电偶极矩产生的。

例3          半径为的导体球置于均匀外电场中，求电势和导体商的电荷面密度。

解：设球外电势为，其通解为

列边界条件

        （1）

                    （2）

（2）式中的C为未知数，其值可由下式求得:

                        （3）

由（1）推出

                             （4）

                          （5） 

由（2）推出

                           （6）

                         （7）

                 （8）

由（5）知，，故由（6）得

联立（4）和（7）得

联立（5）和（8）得

于是

求电荷密度

由（3）得

于是

例4          导体尖劈带电势V，分析它的尖角附近的电场。

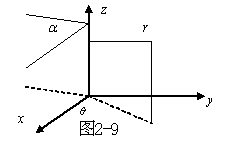解： 采用圆柱坐标系。因电势与z 坐标无关，故拉普拉斯方程为

分离变量

因 ，所以

（为实数）

其解为

于是，电势的通解可写成

考虑边界条件

（1）    在面上，，对任意成立；

（2）    自然边界条件，

（3）    在面上，，对任意成立。

由（1）得

 

由（2）得

由（3）得

重写电势

注意的确定还需在某一大的边界面上的边界条件来确定。但可以用此式来研究尖劈附近的电场分布。

当时，和项中起主要作用，故

尖劈上的电荷面密度为

可以看出，在尖劈附近场强，且有较大的电荷密度。

作业：

§2.4   镜象法

1．镜象法的依据

当所求区域有自由电荷时，需要求解泊松方程。求解泊松方程通常较繁。

镜象法的依据：

  所求区域有点电荷或其它形式的电荷分布，边界是导体或介质界面。用虚拟电荷模拟感应电荷或束缚电荷产生的场，与真实电荷一起，共同满足所给的边界条件。根据唯一性定理，它们所产生的场即为所求的场。

2．举例

例1 接地无限大平面导体板附近有一点电荷Q，求空间中的电场。

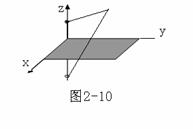解：建立直角坐标系，如图所示。明确所求区域为上半平面。边界条件为

做虚拟电荷，其位置与电量如图所示。

场点的电势为

由边界条件得

于是

 

通过上例，应用镜象法时应注意：

（1）    在所求区域内不应存在虚拟电荷，否则会影响泊松方程。

（2）    构造虚拟电荷来满足给定的边界条件，即由边界条件来确定虚拟电荷的电量和位置；

（3）    考虑虚拟电荷的效果，就不应考虑感应电荷或束缚电荷的效果；

（4）    虚拟电荷可能不止一个。

例2 真空中有一半径为的接地导体球，距球心为（）处有一点电荷Q，求空间各点的电势。

解： 设虚拟电荷的电量为，位于距球心处，Q 与共同作用满足边界条件

考虑边界条件，有

可以看出要使上式满足，须使

即有

于是

称为镜像电荷。

空间中任意点的电势为

例3 如上例，但导体球不接地而带有电荷。求球外电势，并求电荷所受的力。

解： 对于本题，导体电势未知，但知道球面所带电量。为了保证从球面上发出的电通量为，又要保证球面为等势面1，除了镜像电荷外，还应在球心放一虚拟电荷。于是，球外任意点的势为

点电荷受到的力为

=

当时，上式第二项重要，，出现吸引力。

§2.5   格林函数（略）

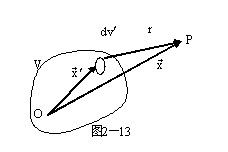§2.6   电多极矩

1．电势的多极展开

电荷分布在真空中产生的电势为

令

假定电荷分布在很小区域，或场点远离电荷分布，则可把进行展开。应用公式

我们可以得到

将其代入电势公式得

令

-------------------------总电量

----------------------电偶极矩

---------------电四偶极矩

于是

-------------------------------点电荷产生的电势

----------------------电偶极矩产生的电势

-------------电四偶极矩产生的电势

可以看出，当R较大时，电势随着极矩阶数的增大而迅速减小，故更高阶极矩产生的电势可以忽略。

2．电多极矩

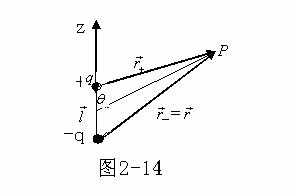
（1）电偶极矩产生的电势

下面阐明为何上式可以看作电偶极矩产生的电势。考虑一个电偶极子，如图所示。

当时，有

这是一个沿z方向的电偶极矩产生的电势。

（2）电四偶极矩产生的电势

先讨论量。成为电四偶极矩张量分量，共有9个分量。电四偶极矩也可写成并矢的形式

 

由于，故为对称张量。又因，故只有5个独立分量。

  下面研究一种电四偶极矩产生的电势。

 

说明：

因而展开式的第三项确为电四偶极矩产生的电势。需要说明电四偶极矩还有其它的分布方式，见教科书。

3．电荷体系在外电场中的能量

设外电场电势为，可以证明，电荷分布在外电场中的能量为

对于小的电荷分布，下面近似计算相互作用的能量。取坐标原点在电荷的内部，将电势在坐标原点附近展开

相互作用能为

第一项：，为电荷集中在原点时的能量；

第二项：，为体系电偶极矩的能量；

电偶极矩在外场中受到的力为

电偶极矩在外场中受到的力矩为

第三项：，为为体系电四偶极矩的能量。

可见在非均匀电场中电四偶极矩的能量才不为零。

本章小结

1. 已知真空中电荷分布，求电势

 

2. 已知电场分布，求电势

3. 已知电势求电场

  

4.        泊松方程和拉普拉斯方程

  

5．唯一性定理

  （）

若电势电势的法向导数已知，则上述方程有唯一解。

6．电势满足的边值关系

  ，

式中从介质1指向介质2。

一侧为导体，另一侧为介质，则有

，

7．理想导体的性质

（i）                导体内无电场；（ii）导体表面为等势面。

8．球坐标系下的分离变量法

  ，

若电势具有轴对称性，即电势与方位角无关，则通解为

若电势具有球对称性，即电势与方位角无关，则通解为

9．镜像法

要点：构造虚拟电荷，与真实电荷一起满足边界条件。对球形边界的镜像关系有

，。（互为镜像）

10．            电偶极子的电势的计算

    

11．            电偶极子的电势的计算