电动力学
主讲人:王中结
【教学目的】
通过本章教学,使学生了解静磁场的特点以及描述静磁场的两个基本方程、矢势的意义及其满足的泊松方程、磁标势概念、磁多极展开,静磁场与静电场的比较。
【重点难点】
球坐标系的分离变量法和镜像法。
第三章 静磁场
§3.1 矢势及其微分方程
1.静磁场的矢势
(1) 描述静磁场的基本方程
微分形式:![]() ,
,![]()
积分形式:
![]() ,
,
![]()
由于静电场的无散性,![]() 的磁力线并不终止于某个地方,说明磁力线是闭合的。
的磁力线并不终止于某个地方,说明磁力线是闭合的。
(2) 矢势的引入

![]()
(3) 矢势的物理意义
如图所示,考虑一个开面的积分,
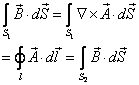
穿过![]() 的磁通量等于穿过
的磁通量等于穿过![]() 的磁通量,这说明
的磁通量,这说明![]() 是闭合的。
是闭合的。
矢势的物理意义
穿过以![]() 为边界的磁通量等于矢势的环流。
为边界的磁通量等于矢势的环流。
(4) 矢势的非唯一性
可以看出矢势![]() 与矢势
与矢势![]() 对应同一个磁感应强度
对应同一个磁感应强度![]() 。
。
![]()
这样一来,引入矢势就毫无意义。为此,必须对矢势施加限制。
(5) 规范条件
库仑规范条件
![]()
下面可以证明做到这一点。
假定![]()
可取另一解![]() ,使
,使
![]()
于是
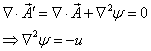
由上式可知,总可以找到一![]() 使
使![]() 。
。
采用库仑规范的优点
(1)
使![]() 建立一一对应得关系,但相差一个常量;
建立一一对应得关系,但相差一个常量;
(2)
对于均匀磁场,![]() 仍不存在一一对应得关系;
仍不存在一一对应得关系;
(3)
使关于![]() 的微分方程简化。
的微分方程简化。
2.矢势微分方程
![]()
![]()
利用库仑规范条件,得
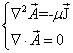 ------------------称为泊松方程
------------------称为泊松方程
下面泊松方程的特解
与标势泊松方程及其解
![]()
比较,可得矢势泊松方程的特解
![]()
可以验证这个解得正确性。
![]()

上式即为毕奥-萨法尔定律。
3.矢势边值关系
出发点是电场的边值关系
![]() (1)
(1)
![]() (2)
(2)
利用上式,可得两介质分界面上矢势边值关系为
![]() (3)
(3)
![]() (4)
(4)
若矢势满足库仑规范条件,则可导出更简单的矢势边值关系
做回路如图所示,计算磁通量
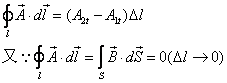
![]()
另一方面,若取![]() ,则有
,则有
![]()
故有
![]()
综合之,可得
![]()
4.静磁场的能量
磁场总能量为
![]()
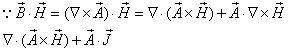
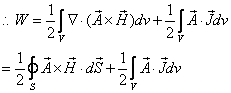
![]()
故当![]() 时,上式中的第一项为零。因此有
时,上式中的第一项为零。因此有
![]()
5.举例
例1:无限长直导线载电流I,求磁场的矢势和磁感应强度。
解:建立坐标系,如图所示。注意矢量位的方向与电流方向一致。


当![]() 时,
时,
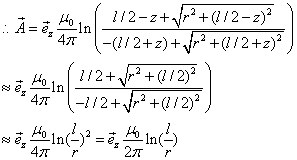
说明当![]() 时,矢量位
时,矢量位![]() 。这是因为我们把无限远处的矢量位规定为零的缘故。
。这是因为我们把无限远处的矢量位规定为零的缘故。
我们可以在矢量位上加一常数![]()
于是
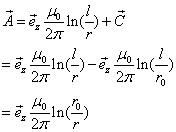
再求磁感应强度
![]()
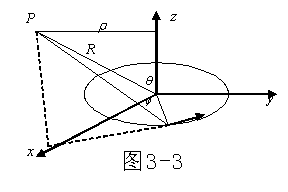
例2:半径为![]() 的导线圆环载电流I,求矢势和磁感应。
的导线圆环载电流I,求矢势和磁感应。
解:
[分析]建立求坐标系,如图所示。因矢势![]() 只有
只有![]() ,且与坐标
,且与坐标![]() 无关,故场点可选在
无关,故场点可选在![]() 平面(
平面(![]() 平面)中。
平面)中。
先求矢势:
![]()
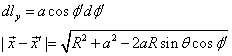
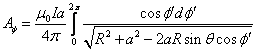
此积分可用椭圆积分表示。
下面采用近似方法,进行积分。
当![]() ,有
,有
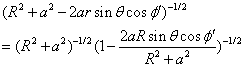
![]()
![]()
由于![]() ,所以
,所以![]()
![]()
当![]() 时(近轴近似),再圆柱坐标系中有
时(近轴近似),再圆柱坐标系中有
![]()
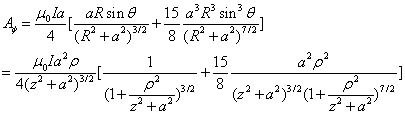
![]()
取![]() 的旋度,得
的旋度,得
![]()
![]()
对于近原点场,![]() ,有
,有
![]()
![]()
§3.2 磁标势
1.引入磁标势的可能
通常求矢势仍较麻烦,对于静磁场,是否可以引入一个标量势,回答是肯定的。大家知道
![]()
若在所求空间中,没有电流与回路相铰链,则
![]()
磁场是无旋的,故可与电场类似引入一个标量势![]() 。
。
引入磁标势的条件:![]()
例如,对于螺旋管线圈,在其内部无电流,磁场的旋度为零;又如在两磁极之间,甚止在磁铁内部,也无自由电流分布,故磁场的旋度亦为零。
引入磁标势的根本原因:
磁场总体上是有旋的,但局部可以是无旋的。
想一想: 对于一个电流线圈,在挖掉电流线圈的剩余区域,能否引入磁标势?
2.磁标势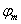
在![]() 区域,有
区域,有
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
由(1)可引入
![]()
3.磁荷
将(3)代入(2)得
![]()
定义磁荷密度
![]() (与束缚电荷密度比较
(与束缚电荷密度比较![]() )
)
我们得到
![]() (与
(与![]() 比较)
比较)
注意:无自由磁荷
磁标势满足的方程为
![]()
磁标势边值关系
![]() (此条件由
(此条件由![]() 推出)
推出)
![]() (此条件由
(此条件由![]() 推出)
推出)
4.磁标势法有关公式与静电场公式比较
|
静电场 |
静磁场( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
结论:用静电场的方法来分析静磁场问题,如分离变量法,镜像法等。
5.应用举例
例1
证明![]() 的磁性物质表面为等势面。
的磁性物质表面为等势面。
 解:设介质1,2的磁场分别为
解:设介质1,2的磁场分别为![]() ,满足边界条件
,满足边界条件
![]()
可知
![]()
![]()
![]()
![]()
因而介质表面为一等势面。
注意:可通过选择磁极表面的形状来获得不同形式的磁场。
例2
求磁化矢量为![]() 的均匀磁化铁球所产生的磁场。
的均匀磁化铁球所产生的磁场。
解:[分析] 磁介质球将产生束缚磁荷。
 磁荷密度为
磁荷密度为
![]()
故磁荷分布在介质球的表面上。
设介质球内外的磁标势分别为![]() ,且
,且
![]()
注意磁标势的轴对称性,写出通解为

列边界条件
在无穷远处磁标势应取有限值,故
![]() (1)
(1)
在![]() 时,磁标势也应有限,故
时,磁标势也应有限,故
![]() (自然边界条件)
(2)
(自然边界条件)
(2)
在介质球面上,有
![]() (3)
(3)
由![]()
![]() (4)
(4)
由(1)推出
![]()
由(2)推出
![]()
重写![]() 为
为

由(3)和(4)得
![]()
![]()
比较两边![]() 的系数,得
的系数,得
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
联立(5)和(7),解得
![]()
联立(6)和(8),解得
![]()
于是

![]() 还可以表示成
还可以表示成
![]() 为总磁偶极矩。
为总磁偶极矩。
球内磁场强度为
![]()
球内磁感应强度为
![]()
球内磁场强度为
![]()
§3.3 磁多极矩
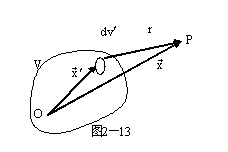 1.矢势的多极展开
1.矢势的多极展开
电流分布![]() 在真空中产生的矢势为
在真空中产生的矢势为
![]()
令![]()
![]()
![]()
假定电流分布![]() 在很小区域,或场点远离电流分布,则可把
在很小区域,或场点远离电流分布,则可把![]() 进行展开。与电势的讨论类似,我们可以得到
进行展开。与电势的讨论类似,我们可以得到
![]()
将其代入矢势公式得
![]()
![]()
![]()
![]()
![]()
![]() (针对一个电流线圈来分析)
(针对一个电流线圈来分析)
![]()
![]()
![]()
![]()
![]()
![]()
式中
![]() (称为电流线圈的磁矩)
(称为电流线圈的磁矩)
对体电流分布,则有![]() 。
。
2.磁偶极矩的场和磁标势

可以证明在电流区域之外的磁场可用磁标势来描述。


3.小区域电流分布在外磁场中的能量
设外磁场电势为![]() ,可以证明,电流分布
,可以证明,电流分布![]() 在外磁场中的能量为
在外磁场中的能量为
![]()
![]()
对于小的电流分布,下面近似计算相互作用的能量。取坐标原点在电流的内部,将磁感应在坐标原点附近展开
![]()
![]()
相互作用能为

可以证明小电流线圈在磁场中的势能为
![]()
磁偶极子在外磁场受到的力为
 (
(![]() 的源不在线圈原点,故
的源不在线圈原点,故![]() )
)
还可以求出线圈在磁场中受到的力矩为
![]()
本章小结
1. 已知真空中电流分布,求矢势
![]()
2. 已知矢势求磁感应
![]()
3. 矢势微分方程和库仑规范
![]()
4. 矢势满足的边值关系
![]()
5. 静磁能的一种计算方法
![]()
6.磁标势
![]()
可以用静电场的方法求磁场。
7.磁偶极矩的势和场
![]()
