【教学目的】

通过本章教学，使学生了解平面电磁波的特点，平面电磁波在理想介质、导体、分层介质、波导中传播时的特点以及谐振腔的工作原理。

【重点难点】

电磁波在导体、分层介质、波导中传播过程的分析。

第四章  电磁波的传播

§4.1   平面电磁波

1．电磁场波动方程

麦克斯韦方程组

，，，

再加上物质方程

构成了研究电磁波问题的基础，如电磁波的产生与传播等。

在自由空间中（），麦克斯韦方程组化为

，，，

可以看出，电场与磁场相互激发，将会以波的形式传播。

（1）在无源真空中

，，，

于是

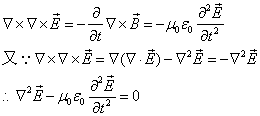
令

则

同理，有

可以看出，电磁场满足波动方程，为电磁波在真空中的传播速度。

（2）在无源介质中

在介质中，物质方程

通常并不成立。实验表明，与电磁波的频率有关，故有

式中分别是的富里叶分量。

2．时谐电磁波（单色波）

（1）时谐电磁波定义

   以一定频率作正弦振荡的电磁波，称为时谐电磁波，如载波，激光束等

（2）时谐电磁波的数学表示

  

  

式中，是复数，称为复振幅。

由于与有一一对应的关系，故写成

（已省除下标和“”）

同理有

，，

（3）时谐情形下的麦克斯韦方程组

注意：

（1）    上述方程组中场量表示复振幅，其瞬时表示，需乘以因子再取实部；

（2）    当时，上述方程组只有两个是独立的。

（4）亥姆霍兹方程

  

   ----------------亥姆霍兹方程

   注意：上述亥姆霍兹方程的解只有满足才代表电磁波的解。

电磁波的另一个场量可由下式得出

  

  在无源空间中，时谐电磁波问题的分析由下式描述

 

同理有

 

3．平面电磁波解

（1）平面电磁波解

     假定电磁场振幅仅与坐标有关，而与无关，即，，则亥姆霍兹方程化为

  

其解为

   ，为常矢量

其瞬时表示式为

上式中称为相位因子。根据前面的分析，这个平面波需满足条件

这说明电磁波的振动方向与传播方向垂直，即电磁波为偏振波。

（2）平面电磁波的相速与色散效应

画出电磁波的波形，如图所示。

在时刻，有

在另一时刻，有

我们发现相位的波峰移到处。因此，波峰传播速度为

---------------电磁波的相速。

在真空中，相速为

在介质中，相速，与电磁波频率有关。

容易看出两相邻的波峰之间的距离，即波长为

式中称为波数。

色散效应：在介质中，电磁波的相速与其频率有关，称为色散效应。

（3）平面电磁波的一般表示式

  电磁波的相位面：由相同的电磁波相位构成的面。若电磁波的相位面为平面，则称为平面波。显然，相平面与传播方向垂直。

对于任意的传播方向，平面波如图示，其表示式为

  

式中，指向传播方向，称为波  矢。

由电磁波的横波条件得

说明电磁波有两个独立的偏振方向。

平面电磁波的磁场分量为

或

由此可以看出

（4） 平面电磁波的特性

（i）电磁波为横波（偏振波），

  （ii）

  （iii），

 4．电磁波的能量和能流

电磁波的能量密度为

对于在线性介质中时谐电磁波，有

对于平面电磁波，有

这说明平面电磁波的电场能量与磁场能量相等。于是

平面电磁波的能流

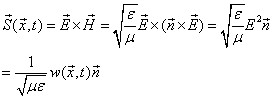
下面计算一个周期内电磁波的能量与能流的平均值

同理，电磁场平均能流蜜度为

下面给出一个正弦变化量的平均值的计算方法：

若

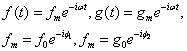
§4.2   电磁波在介质界面上的反射和折射

1．反射和折射定律

 研究电磁波在介质界面上的反射和折射的出发点是电场的边值关系。

 

研究电磁波在无源介质中的传播，，且上述四个边值关系中只有两个是独立的（因麦氏方程也只有两个是独立的），故取

                  （1）

                 （2）

  下面研究反射和折射现象

假定入射波是平面波，反射波和折射波也是平面波，如图所示。

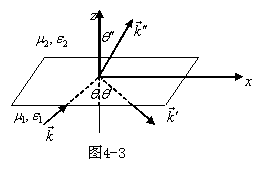
介质1中的场强为

介质2中的场强为

根据边界条件（1），得

两边的实部和虚部相等，得

---------------------称为相位边值关系

-------------------称为振幅边值关系

同理对磁场分量也有类似的关系。

-------------------称为振幅边值关系

而相位边值关系与电场分量相同。

设分界面为面，由相位边值关系得

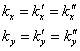
假定入射波矢位于平面，即，则

故反射波矢和折射波矢也位于平面。由图知

， ，

由得

-----------------------反射定律

由得

（对非铁磁介质有）

---------------折射定律

这进一步说明光是一种电磁波。

 

 

2．振幅关系  菲涅尔公式

下面利用振幅边值关系研究反射波和折射波与入射波的振幅关系。分两种情形讨论。

（1）

如图所示，振幅满足

 

（已略除下标）

当时，有

                    eq \o\ac(○,1)1

      eq \o\ac(○,2)2

注意到入，反，折射波均为平面波，有

代入（2）得

          eq \o\ac(○,3)3

联立（1）和（3），并应用反射定律，可得

上式为菲涅尔公式。

（2）

如图所示，利用振幅边值关系，可得

与上同样推理，得菲涅尔公式

（3）讨论

（i）布儒斯特角。

    当时，的反射光消失。反射光为完全偏振光。

（ii）半波损失。

    若，则。此时，对入射面的情形，有负数。这说明在分界面处反相。这种现象称为半波损失。

（iii）其它形式的偏振可将场量分解为平行入射面和垂直入射面来加以讨论。

2．全反射

现在讨论，即光从光密介质进入光疏介质的情形。

则。

当时，有

进一步增大入射角，使，则

此时光发生全反射，折射光消失。事实上，折射光仍存在。下面导出折射光的形式。

利用相位边值关系

 设

注意到

所以，折射波的场强为

这是一个衰减波。

穿透深度为

还可以算出折射波的能流。

在情形下，有

还可以求出反射波与入射波的振幅比

§4.3   有导体存在时电磁波的传播

1．导体内的自由电荷分布

在导体中，对于时变场，存在这样几个基本方程

利用上述方程，可以研究讯变场作用下导体内自由电荷分布。

结论：自由电荷体分布随时间衰减。当时，，说明导体内不存在自由电荷分布，电荷分布在导体表面上。

定义特征时间为

 

对于电磁波，若小小于电磁波的一个周期，即

                   （1）

导体内自由电荷分布在特征时间内，有

我们把这样的导体称为良导体。

良导体的条件为

1．导体内的电磁波

（1）导体内的频域麦氏方程

在导体内，有

，

，

，

对于时谐电磁波，有

定义“复电容率”为

于是

这样电磁波在导体中传输问题可仿照介质方式处理。

（2）复电容率的物理意义

假定绝缘介质不存在损耗，即为实数。

位移电流密度：

传导电流密度：，这个量与复电容率的虚部有关。

位移电流的平均损耗功率为

传导电流的平均损耗功率为

结论：复电容率的虚部代表损耗。

（3）导体中亥姆霍兹方程的解

   导体中亥姆霍兹方程为

 

其解为

可以看出，电磁波在导体中传播存在率减。称为衰减系数，称为相位常数。

下面求。

比较两边的实虚部，得

               （1）

                （2）

通常的方向并不一致，由上两式还不能确定，还需利用相位边值关系。

例如，考虑电磁波气中射入导体，如图所示。

设入射面为平面，为入射波矢，为折射波矢，由相位边值关系得

为实数，

再由（1）和（2）确定。

 

3．穿透深度与趋肤效应

考虑电磁波垂直入射导体情形，如图4-7所示。

根据前面的分析，有，所以透射波为

由

               （3）

                （4）

解得

对于良导体，，有

定义穿透深度

得

以金属铜为例，，当当

这说明电磁波频率越高，穿透深度越小。电磁波在良导体中只存在在其表层中。这种现象称为趋肤效应。

4．良导体中电磁波的电场分量与磁场分量间的相位关系

在良导体的情形下，有

（在良导体中）（在介质中）

结论：

（i）                   电磁波在良导体中传播时，的相位落后的相位；

（ii）                 导体中的电磁波，起主要作用。

5．导体表面上的反射

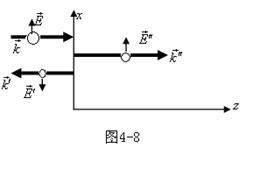
下面只讨论垂直入射情形，如图所示。

假定沿方向，即入射面。根据振幅边值关系，有

              （1）

             （2）

 

对于良导体，有

将其代入（2），得

 

    （3）

解得

定义反射系数

对于良导体，有

电磁波几乎被良导体反射，良导体可以作为电磁波的边界。

6．应用举例

例1 试证明在良导体内，非垂直入射情形有

    

证：如图所示，由相位边值关系，得

 

在良到体内，有

由

例2 计算高频下良导体的表面电阻。

解：导体内的电流密度为

设，电磁波沿z方向传播，如图所示。

因为电流只分布在的薄层内，故可看作面电流分布。设为单位横截线的电流密度，则

（因，很小，积分可以扩展到无限大）

导体表面平均损耗功率密度为

导体表面单位损耗功率为

作业：P180,5,6,7

§4.4   谐振腔

1．有界空间中的电磁波

导体能约束电磁波，这是由于导体使电磁波不易穿透。因此可利用金属管道使电磁波定向传输，利用金属空腔产生高频电磁波振荡。分析这类问题时，通常导体的作用作为边值问题来处理。

2．理想导体的边界条件

（1）两个介质界面的边界条件

对电磁波而言，上述四个方程只有两个是独立的。通常取

（2）一侧为导体另一侧为介质的边界条件

若1侧位导体，导体内的场量可忽略，则边界条件为

（3）以导体为边界的电磁波问题的解

由于处处成立，在导体表面上亦成立，故有。

（4）电磁波的模式

（i）TEM模式

     电磁波的电场，磁场均垂直于传播方向。

（ii）TE模式

     电磁波的电场垂直于传播方向，但磁场不垂直。

（iii）TM模式

     电磁波的磁场垂直于传播方向，但电场不垂直。

（5）举例

证明两平行无穷大导体平面之间可以传播一种偏振TEM电磁波。

证: 选择坐标系如图所示。设电磁波沿z方向传输。

 

由边界条件，

可得

（在两导体板间）

另一方面，由

结论：可以存在TEM波。

3．谐振腔

（1）谐振腔

一种产生高频电磁振荡的金属装置。

对于LC回路，振荡频率为

振荡频率越高，须减小L，电感用片状来代替丝状；进一步减小L，须用多片状并联。

（2）谐振腔振荡模式和频率

根据亥氏方程

设为的任意分量，则

应用分离变量法

，，

寻求驻波解（因存在反射）

用边界条件确定待定常数

先考虑的情形

于是

同理

再利用另一组边界条件

于是

另一方面，因，可得

故只有两个是独立的，它们由初始条件来决定。

一种组合称为一种模式。

谐振频率

称为谐振腔的本征频率。

讨论：

（i）                   若有两个为0，则，故不存在这种模式；

（ii）                 若，则最低本征频率的模式为，其频率为

§4.5   波导

1．高频电磁能量的传输

波导：一种产生高频电磁振荡的金属装置。

在低频的情形下是双线传输，在高频情形下则是波导。

2．矩形波导中的电磁波

根据亥氏方程

 

设电磁波沿z方向传播，则

代入亥氏方程，得

设为的任意分量，则

应用分离变量法

，

 

寻求驻波解（因存在反射）

用边界条件确定待定常数

先考虑的情形

于是

又由于

同理

利用公式，，还可以求出

讨论：

（i）不能同时为0；

（ii）

（iii）                矩形波导中只能传输TE，TM模式。理由是

       

         可以看出，不能同时为0。

3．截止频率

满足时的电磁波的频率称为截止频率。截止频率为

可以看出，截止频率取决于波导的尺寸和电磁波的模式。

讨论：

（i）                   若，则

     

电磁波可沿z方向无损耗的传输。

（ii）                 若，则

      为纯虚数

电磁波沿z方向衰减，波导不能传输电磁波。

4．波的电磁场与管壁电流

若，则波的截止频率最小。容易求得波的场量分布。

还可以求出管壁电流。（略）

作业：P180:9,10,13

本章小结：

1．波动方程

2. 频域麦氏方程

  

3.      亥氏方程

  

4.    平面电磁波及其特点

   

5.    电磁波的平均能流

  

6．反射与折射定律得推导

  -----------------------反射定律

---------------折射定律

7．菲涅尔公式

  

8．非稳定时导体内的自由电荷分布

9．复电容率

 

10．良导体中的衰减系数与相位常数以及电场与磁场的关系

 

 

11．谐振腔的振荡频率

  

12．波导的截止频率