【教学目的】

通过本章教学，使学生了解相对论的时空观，电动力学的相对论协变性以及相对论动力学方程。

【重点难点】

相对论的基本原理，洛伦兹变换，速度变换公式，能量—动量四维矢量，相对论动量守恒定律。

第六章    狭义相对论

§6.1   狭义相对论的实验基础

1．相对论产生的历史背景

黑体辐射量子理论（1901，普朗克）

以太绝对参照系的否定狭义相对论（1905，爱因斯坦）

2．迈克尔孙-莫雷实验

这个实验否定了以太绝对参照系，证实伽利略速度合成法则失效（至少对光速而言）。实验装置如图所示。M为半透半反镜片，为补偿镜片，为反射镜。干涉仪由于地球的自转做相对于以太以速度运动。光在以太中的速度为。光相对于地球的速度为。按伽利略速度合成法则，则为

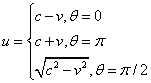
下面求各支路的光程，为此先求各支路传播时间。

支路的传播时间

支路的传播时间

两支路间的光程差

将整个干涉仪旋转，两支路间的光程差

干涉条纹移动的条数为

取，得

实验观察到，干涉条纹几乎不移动。这说明了什么？

这说明不存在以太绝对参照系，伽利略速度合成法则失效，也意味着牛顿经典理论存在局限性。为了保证伽利略速度合成法则有效，洛伦茨提出了一种解释。

  他假定在的方向上，缩短到。若这样，则有

光程差：

但这种解释有点差强人意。后来，爱因斯坦提出了一个系统的理论，解释了为何不存在干涉的原因。

§6.2   相对论的基本原理 洛仑兹变换

1．相对论的基本原理

（1）相对性原理

  所有惯性系都是等价的，物理规律（不仅仅是力学规律）在各惯性系中有相同的形式。

（2）光速不变原理

   光速在各惯性系中均相同，且与光源的运动无关。

前一个假设是把惯性系推广到一般情形，后一个假设认定光是自然界中最快的速度。

  由这些假设出发，会引出令人不可思议的结果，如同时性的相对性。考虑位于地面（看作惯性系）两个接收器中点的光源在某一时刻发出光脉冲，如图所示。设以速度运动的火车（惯性系）。按经典理论解释，光脉冲在两个惯性系中看来均同时到达接收器（同时性的绝对性），但是按相对论观点，由于光速不变，在中看来，光先到达，后到达点，故不同时。这叫同时性的相对性。

2．间隔不变性

（1）事件

   在空间某点和时间的某一时刻发生的物理过程，称为事件，

如光脉冲的发出，粒子的运动等，用空时坐标表示。

在另一惯性系中，则用。

（2）事件间隔

设两事件在中分别为，则两事件的时空间隔定义为

   

在中，则两事件间隔为

对光信号而言，有

在中，因，故。

在中，因，故。

因此，对光事件有

对于一般事件，是否也成立？回答是肯定的。

（3）间隔不变性

定义二次型函数

设两惯性系中的坐标是线性变换关系，作的变换，依据数学上的定理，线性变换时二次型函数的形式不变，故

由于空间各向同性，因子仅与惯性系间的相对速度大小有关。

另一方面，作反变换，则有

 

于是

解得

为保持变换的连续性，我们取。

于是

上式体现了两个基本假设：规律的协变性和光速不变性。

3．洛仑兹变换

设两惯性系空时坐标的变换关系为

由间隔不变性，得

比较两边系数得

由（1）和（3）得

为了回到经典情形，要求。

由（2）得

另一方面，我们研究原点的运动。显然有

最后得

于是坐标变换为

逆坐标变换为（）

注意：坐标变换不具有传递性。

例 如图所示，设闪光从O点发出，在上观察，光讯号于1秒之后同时被接收。设相对于的运动速度为，求接收到讯号时的时刻和位置。

解：点在上的空时坐标为，由洛氏变换得

 

故得在上的空时坐标

对于，同理有

在中：

在中：

可以看出：两事件在是同时发生，但在中是不同时发生的；还可以看出对于这样的两事件。

§6.3   相对论的时空理论

1．相对论的时空结构

讨论两事件的间隔，一个位于原点，另一个位于。这两个时间的间隔为

，为两事件的空间距离。

假定两事件由粒子的运动相联系，设粒子运动速度为，，。

（1）   三种间隔

（2）   三种间隔图示

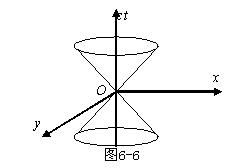取，间隔图示如图所示。分三种情形讨论：

（i）                   在光锥表面上任意点，有，故锥表面

    为类光间隔。

（ii）                 在光锥内部，有，故光锥内部为类时间隔。

注意：若两事件间隔位于上半光锥，则在其它参照系看来，仍位于上半光锥。上半光锥称为绝对未来；下半光锥称为绝对过去。

（iii）                在光锥外部，有，故光锥外部为类空间隔。

注意：若两事件间隔位于光锥外，且发生在不同的地点，则在其它参照系看来，仍发生在不同的地点。因而两事件具有绝对异地。

 

2．因果律和相互作用最大传播速度

因果律：两事件有内在联系，先有因后有果。

下面我们在上半光锥中讨论因果性。

设在中有两事件和，。在中看来两事件的空时坐标分别为和。根据洛氏变换，得

若两事件的联系速度（或叫相互作用传播速度）满足

也可看作相互作用传播速度，则

即保持了因果性。

结论：若保持因果性，则相互作用传播速度应小于光速。

3．同时相对性

下面我们在类空时空中研究同时性问题。

设在中有两事件和，（不同时）。由于两事件是类空的，故有

在中看来两事件的空时坐标分别为和。根据洛氏变换，得

若足够大，则有

于是有

（因果性失效，两事件无内在联系）

若选择另一参照系以速度相对运动，满足

则有

（同时性）

由于同时相对性，因而存在时钟校准问题，可采用缓慢移动时钟方法解决。

4．运动时钟的延缓

设有一个运动的钟，固定在钟上（处）。有两个事件和，可理解为原子钟周期的起点和终点。两事件时空间隔为

在中看来

事件1发生在，（钟与比较）

事件2发生在，（钟与比较）

其时空间隔为

根据间隔不变性，故有

又

称为原时或固有时（时钟静止时的读数），为中看到的运动钟的读数。可以看出，运动时钟走得慢。

例如，若，则，即上时间流逝1秒，在上则流逝10秒。

时钟延缓效应已在高能物理实验中得到证实。

讨论：

（i）                   对于匀速运动，时钟延缓效应是相对的。即在中看中的钟也变慢。

观察者在中时，他看到的中的两个钟将不再同时，因而不能直接比较。须在中设置两个钟，如图所示。

开始时，与相遇比较（事件1），经过一段时间后，与相遇比较（事件2）。这两事件的空时坐标为

：

：

根据洛氏变换，有

可以看出，。即在中看中的钟也变慢。

（ii）                 对于加速运动，时钟延缓效应是绝对的。

（iii）                时钟延缓效应是由时空基本属性引起的。

5．运动尺度的缩短

在运动的尺子上建立参照系，其长度为。在中去测量尺子的长度。测量时要注意同时性，即（这可通过闪光的办法达到）。根据洛氏变换

又

式中为运动尺子的长度。

结论：运动尺子存在缩短效应，是由时空结构引起的。已得到实验证实。

6．速度变换公式

设中粒子的速度为

中粒子的速度为

设相对以速度沿方向运动，则

对上式两边取微分，得

于是可得

速度逆变换为（）

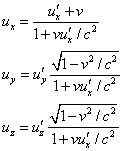
讨论：

（i）                   在经典极限下，即，则有

        

（ii）                 若，则有

        

例  求匀速运动介质中的光速。

解： [分析] 对于运动介质，设其静止折射率为，光在静止介质中的传播速度为。将建立在运动介质上。

又设光沿方向传播，根据速度合成公式，得

作业：P290,2,3,4

 

§6.4   相对论理论的四维形式

1．三维空间的正交变换

（1）二维空间的正交变换

设坐标系为绕z 轴旋转一角度所得。任意点P在两个坐标系中关系为

，

同时OP长度不变，即有

对于任意矢量，也有同样的变换。设中，中，两者关系为

正交变换：保持矢量长度不变得变换称为正交变换。

（2）三维正交变换

设中P点坐标为，中，两者关系为

                 （1）

转动时，OP长度不变，即

（正交条件）  （2）

变换（1）可以写成求和形式

采用爱因斯坦求和约定—重复下标表示求和，则上式可写成

                              （3）

正交条件（2）表示成

将（3）代入上式，得

                        （4）

引入符号

由（4）得

（正交条件）

下面求正交变换的逆变换。

正交变换还可以写成矩阵形式。定义矩阵

，，

则正交变换为

定义转置矩阵，则正交条件的矩阵形式为

式中I 为单位矩阵。

2．物理量按空间变换性质分类

（1）标量

 物理量与空间坐标无关或在空间中没有取向关系，这样的量称为标量，如质量，电荷等。标量在坐标变换下保持不变，即

（2） 矢量

 物理量在空间中有一定的取向性，可用三个分量表示，如速度，力等。其变换关系为

注意算符也具有矢量性质，矢量的标积变换时不变。

（3）   二阶张量

有些物理量具有复杂的空间取向性，称为二阶张量，如电磁场动量流张量。二阶张量按下列变换规则变换

张量可以写成并矢形式：

张量变换有下列性质：

（i）                   对称张量变换后仍为对称张量；

（ii）                 反对称张量变换后仍为反对称张量；

（iii）                张量的迹变换时不变。

定义张量的迹：，变换后的迹为

3．洛仑兹变换的四维形式

前已提出，对于三维坐标系得转动，有

使

或写成

在相对论四维时空中，在坐标变换下，我们有间隔不变性

         （1）

定义第四维坐标

于是（1）写成

结论：洛仑兹变换相当于四维空间的正交坐标变换。

洛仑兹变换的四维形式为

式中，

洛仑兹变换的四维形式还可以写成

。

今后用希腊字母表示1~4。

4．四维协变量

（1）协变量

  在四维空间中，可将物理量按其变换性质分类。

（i）                   标量：在洛氏变换下保持不变得量，如时间间隔，固有时等

       

（ii）                 矢量：在洛氏变换下按下列方式变换

，如四维位矢，四维速度等

（iii）                张量：在洛氏变换下按下列方式变换

，如四维电磁张量等

（2）四维速度

 定义四维速度

  

通常速度为

 

同理有

 

于是四维速度表示为

 

讨论：

（i）                   在经典极限下，四维速度的空间分量与通常速度相同；

（ii）                 四维速度的标积为一不变量，即

（iii）                从四维速度的变换可以导出通常速度变换公式。

（3）四维波矢

设在有一电磁波，其频率为，波矢为。在中看来，电磁波的频率为，波矢为。现在研究两者的关系。

大家知道，在平面电磁波可以表示成，电磁波的相位

在中看来，电磁波的相位

可以证明，电磁波的相位由于纪录得是波峰的数目，因而是一个不变量，即

定义四维波矢

由于四维矢量的标积是一个不变量，因此确实是一个四维矢量。

四维矢量按下列规则变换

---------------------波矢变换公式

（4）光行差公式

  研究一束频率为光与x轴间的夹角为方向传播，求在观察到的角度和频率。

代入波矢变换公式，可得

-------------------多普勒公式

----------------光行差公式

反过来

在中有一静止光源，，则运动光源辐射的角频率（在中看）为

在垂直于光源运动方向上观察到光的频率为

---------------横向多普勒效应。

注意：横向多普勒效应是相对论结果，无经典对应。

5．物理规律的协变性

在经典情形下，物理规律可表示为

在另一惯性系中有

在相对论情形下，

在参照系中，物理规律可以用一方程表示为

则在另一参照系中，应有

方程在不同参照系中具有相同的形式，这种要求称为协变性。

作业：P291,5,6,7

§6.5   电动力学的相对论不变性

1．四维电流密度矢量

电荷量是一个不变量，即

体积元的变换为

所以电荷密度的变换

带电粒子运动时，其电流密度为

引入电流密度的第四个分量

则四维电流密度矢量为

注意：四维电流密度矢量把电流密度和电荷密度有机统一起来。

电荷守恒定律

可以写成四维形式

（注意重复下标表示求和）

2．四维势矢量

回顾达朗贝尔方程

 

 

（洛伦次规范条件）

注意到达朗贝尔算符

达朗贝尔方程写成

，             （1）

引入四维势

方程（1）可统一成

或

-----------------达朗贝尔方程的协变形式

洛伦次规范条件

下面讨论四维矢的变换。由四维矢量的变换可得

3．电磁张量

为了把麦氏方程组写成协变形式，我们要引入电磁张量。

，

用四维势表示，则为

引入反对称四维电磁张量

经过简单的推导，得

此量将电场与磁场有机统一起来。

注意：电磁张量为反对称张量，即

下面利用电磁张量写麦氏方程组得协变形式。

            （1）

验证如下：

取，则

            （2）

注意，这里重复下标并不表示求和

验证如下：

取

注意方程（2）个方程，但绝大多数为的无意义方程。

下面讨论电磁场的变换。

仔细去算每一个分量，可得

写成简洁形式

“”，“”表示与惯性系速度相平行或垂直的分量。

上述场量关系可用下列方法导出之。

令，

注意到，由此可以求出的16个分量。

讨论：若，则

4．应用举例

例 求匀速运动的带电荷的粒子的电磁场。

解： 将建立在运动电荷上，电荷相对静止。

式中为中测得的位矢。

在中看来，利用电磁场变换公式，有

现在将中的坐标变换到中来。根据洛氏变换，注意到测量时要同时，则有

讨论：

（i）                   当时

       略去的高阶项，得

              （静电场）

          （运动电荷产生的磁场）

（ii）                 当时

       若场点，则

      

若场点，则

      

结论：电场的空间分布将不再是各向同性的。

5．电磁场的不变量

（1）

（2）

§6.6   相对论力学

经典力学规律在伽利略变换下是协变的，但在洛氏变换下不再是协变的。由于洛氏变换式四维的，必须把物理量扩展到四维形式。

1．能量-动量四维矢量

（1）四维动量

利用四维速度定义四维动量

 

为一标量，称为静止质量。

将四维动量写成

所以

-----------称为相对论动量

显然，当粒子速度，有，回归到经典动量。

下面研究四维动量的第四个分量。

当时，有

显然上式括号中的量具有能量的含义，是常数，这个常量的意义后面将予以讨论。

定义自由运动粒子的能量

 ---------------称为相对论能量

于是。因此四维动量的第四个分量与粒子的能量有关。

（2）粒子动能与粒子静止能量

定义的动能

当粒子速度时，相对论动能就回归到经典动能。

粒子静止能量为。

注意：（i）静止能量是相对论结果，无经典对应；

（ii）静止能量可以转化为其它形式的能量。

总结：

四维动量的表示成

2．动量-能量关系式与结合能

（1）动量能量关系式

由可以构造一个不变量

而

选为与粒子一起运动的参照系，在中有

所以

----------称为动量能量关系式

（2）结合能

由各运动粒子组成一个复合物体时，若整体物体是静止的（），其能量并不等于所有粒子的静止能量之和，即

两者之差被定义为物体的结合能

定义物体静止质量

 

定义质量亏损

于是我们有

上述关系式已被大量核物理实验所证实。

（3） 质能关系式

定义粒子的动质量

于是有

相对论动量就与经典动量形式上一致。

（4）   应用举例

例 带电介子衰变为子和中微子

  

各粒子质量为

 

求介子质心系中子的动量，能量和速度。

解： 在介子质心系中，有

  （介子相对静止）

衰变后子和中微子的能量为

 

由相对论动量能量守恒定律，得

                     （1）

           （2）

由（1）得

代入（2）得

将数据代入之得

3．相对论动力学方程

先看经典牛顿方程

 

由于此量在洛氏变换下不是协变的，应修改为

 

式中为四维力矢量，在低速情形下应过度到经典力。下面研究四维力的第四个分量。

于是

-----------------------相对论动力学方程

下面研究与经典力的关系

注意到

同理有

定义

，称为经典力

-----------------------（1）

注意：

（i） 为经典力，但为相对论动量和能量；

（ii） 力的变换由 按四维矢量规则变换；

（iii）不是所有的力都能写成（1）的形式。洛仑兹力恰好能行。

4．洛仑兹力

（1）带电粒子在电磁场中的运动方程

 在电磁场中粒子受到的力为

 

在相对论情形下，我们构造一个四维力

 

显然，上述定义的力具有协变性，其空间分量为

在经典极限下，

回归到经典力。

带电粒子在电磁场中的运动方程为

式中为相对论动量。

（2）应用举例

例 讨论带电粒子在均匀恒定磁场中的运动。

解： 带电粒子在磁场中的动力学方程为

                  （1）

      （2）

由（2）知

 

由（1）得

              （3）

把

由（3）得

                       （4）

               （5）

由（4）知

因而（）

因此（5）式描述了粒子在垂直于磁场作圆周运动。粒子受到的向心力为

粒子的动质量为，于是

，为回旋半径

回旋运动的角频率为

作业：P297,10,17,18

 

 

 

 

本章小结

1．洛仑兹变换

 

2．事件间隔不变性

   

3．相对论时空结构

4．相对论效应

  （1）运动时钟的延缓效应

 

  （2）运动尺度的收缩效应

 

5．相对论速度变换公式

 

6．物理量的分类

  标量   ，如

矢量：，如四维位矢，四维速度等

张量：，如四维电磁张量等

7．洛仑兹变换的四维形式

 

式中，

8．四维速度

  

9．四维波矢

  

  

10．多普勒公式与光行差公式

  多普勒公式   

光行差公式   

11．四维电流密度矢量

  

  

12．四维势矢量

  

13．电磁场张量

  

14．电磁场变换

  

15．电磁场不变量

   （1）

（2）

16．四维动量-能量矢量

  

17．质能表示式

    ，

18．能量-动量关系式

 

19．四维力矢量

  

20．相对论动力学方程

  

21．带电粒子在电磁场中的动力学方程