|
安徽师范大学 精品课程——量子力学
|
《量子力学》复习提纲
第一章 绪论
1、德布洛意假设：德布洛意假设的内容，德布洛意关系，戴维孙-革末电子衍射实验的结果。
2、德布洛意平面波：
3、光的波动性和粒子性的实验证据。
第二章 波函数和薛定谔方程
1．量子力学中用波函数描写微观体系的状态。
2．波函数统计解释：
若粒子的状态用
描写，
表示在t时刻，空间
处体积元
内找到粒子的几率（设
是归一化的）。
3．态叠加原理：设
是体系的可能状态，那么，这些态的线性叠加
也是体系的一个可能状态。
若体系处于
态，我们讲体系部分处于
态。
4．波函数随时间的变化规律由薛定谔方程给出：
当势场
不显含
时，其解是定态解
满足定态薛定谔方程 
其中 
定态薛定谔方程即能量算符的本征方程。
5．波函数的归一化条件：
。相对几率分布：
，波函数常数因子不定性；相位因子不定性。
6．波函数标准条件：波函数一般应满足三个基本条件：连续性，有限性，单值性。
7．几率流密度
与几率密度
满足连续性方程
8．一维无限深方势阱
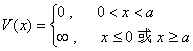
本征值 
本征函数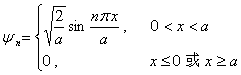 
若 
则本征值 
本征函数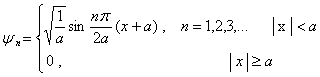 
9．三维无限深方势阱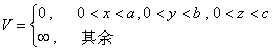 
，
可以用分离变量法求解得到
本征值 
本征函数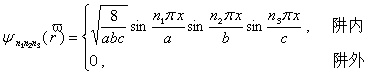 
10．一维谐振子 
本征值 
本征函数 
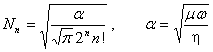
11、可以用分离变量法求解得到（在笛卡尔坐标中）三维各向同性谐振子的能级和波函数。
第三章 量子力学中的力学量
1．量子力学中的力学量用线性厄米算符表示并且要求该算符的本征函数构成完备系。
2.厄米算符
的定义：
厄米算符的本征值是实数。厄米算符的属于不同本征值的本征函数一定正交。
力学量算符的本征函数系满足正交、归一、完备、封闭等条件。
3．力学量的测量值：
在力学量
的本征态中测量
，有确定值，即它的本征值；
在非
的本征态
中测量
，可能值是
的本征值。将
用算符
的正交归一的本征函数展开：
则在
态中测量力学量
得到结果为
的几率为
，得到结果在
范围内的几率为
。
力学量的平均值是
或 
4．
连续谱的本征函数可以归一化为
函数。
5．简并：属于算符的某一个本征值的线性无关的本征函数有若干个，这种现象称为简并。
简并度：
算符的属于本征值
的线性无关的本征函数有
个，我们称
的第n个本征值
是
度简并。
6．
动量算符
的本征函数(即自由粒子波函数)
正交归一性 
7． 角动量
分量 
本征函数 
的本征值
8．
平面转子（设绕
轴旋转）
哈密顿量
能量本征态
能量本征值
9． 
有共同的本征函数—球谐函数
：
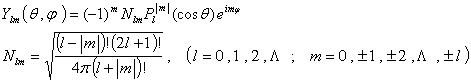
1．
中心力场中，势场
，角动量
为守恒量。
10．中心力场中，定态薛定谔方程
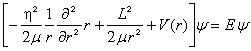
选
为体系的守恒量完全集，其共同的本征函数为
11．氢原子
能级简并度 
轨道磁矩 
磁子
旋磁比 
类氢离子 
12．
守恒力学量的定义：若
（即力学量
的平均值不随时间变化），则称
为守恒量。
力学量
的平均值随时间的变化满足
因而力学量
为守恒量的条件为：
， 且 
13．宇称算符
宇称算符的定义：
，本征值，本征函数。
14． 对易式定义： 
15． 对易式满足的基本恒等式：
（Jacobi恒等式）
16．
一些重要的对易关系：
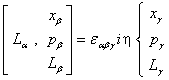
17．若算符
对易，即
，则
和
有共同的本征函数系。在
和
的共同的本征函数表示的态中测量
，都有确定值。
若算符
不对易，即
，则必有
简记为 
特别地， 
第四章 态和力学量的表象
1．
表象是以
的本征函数系
为基底的表象，在这个表象中，有
算符
对应一个矩阵（方阵），矩阵元是
，
选定表象后，算符和量子态都用矩阵表示。
平均值公式是
，
归一化条件是
，
本征值方程是
。
2．
在量子力学中，两个表象之间的变换是幺正变换，满足
；态的变换是
；算符的变换是
。幺正变换不改变算符的本征值。
3．
量子态可用狄拉克符号右矢
或左矢
表示。狄拉克符号的最大好处是它可以不依赖于表象来阐述量子力学理论，而且使用十分方便。
基矢的完备性： 
坐标表象
狄拉克符号
4．粒子占有数表象
以线性谐振子的粒子数算符N或者哈密顿
的本征态
为基矢的表象。
产生算符：
湮灭算符：
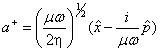
， 粒子数算符：
第五章 微扰理论
1．定态微扰理论
适用范围：求分立能级及所属波函数的修正。适用条件是：一方面要求
的本征值和本征函数已知或较易计算，另一方面又要求
把
的主要部分尽可能包括进去，使剩下的微扰
比较小，以保证微扰计算收敛较快，即
（1）非简并情况
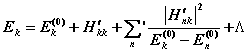
（2）简并情况
能级的一级修正由久期方程
即
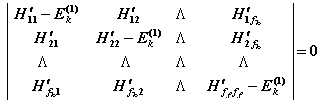
给出。
有
个实根，记为
，
分别把每一个根
代入方程 
，即可求得相应的解，记为
，于是得出新的零级波函数
相应能量为
2．变分法
选择尝试波函数
，计算
的平均值
，它是变分参量
的函数，由极值条件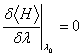
定出
，求出
，它表示基态能量的上限。
3．由
的跃迁几率是
此公式适用的条件是
， 对于
4．周期性微扰：光的吸收和发射，选择定则等。
第七章 自旋与全同粒子
1．电子自旋假设的两个要点：
（
）
；
（
）
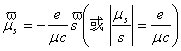
内禀磁矩的值即玻尔磁子的值： 
因子（回转磁比值）： 
斯特恩—盖拉赫实验，
2．旋量波函数
的意义及其归一化。
自旋与轨道无耦合时：
的本征态： 
一般自旋态： 
3．自旋算符与Pauli矩阵 
（单位算符）
, 
, 
， 
， 
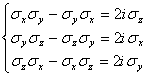
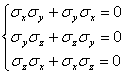
4．总角动量
在中心力场
（例如Coulomb场）中运动的电子的相对论波动方程（Dirac方程），在非相对论极限下，Hamilton量中将出现一项自旋轨道耦合作用
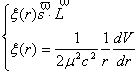
电子的能量本征态可选为（
）的共同本征态，而空间角度部分与自旋部分的波函数则可取为（
）的共同本征态:
本征值分别为
5. 碱金属原子光谱的双线结构
由于
项的存在，使得
。例如
Na：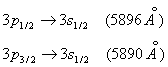 
还可以解释反常塞曼效应。
6．两个电子的自旋单态与三重态
|
（ |
|
|
|
|
|
|
0 0 （单态） |
7. 两个角动量的耦合
若
是两个独立的角动量，则
也是角动量。
C-G系数的性质：
，
j的取值：
8．全同粒子
（1）量子力学中，把内禀属性（静质量、电荷、自旋、磁矩、寿命等）相同的粒子称为全同粒子。
（2）全同性原理：由于全同粒子的不可区分性，使得全同粒子所组成的体系中，二全同粒子相互代换不引起物理状态的改变。
全同性原理或表述为交换对称性：任何可观测量，特别是Hamilton量，对于任何两个粒子交换是不变的。
这就给描述全同粒子系的波函数带来很强的限制，即要求全同粒子体系的波函数具有交换对称性
或者交换反对称性
。
（3） 全同粒子系的波函数的交换对称性与粒子的自旋有确定的联系。
玻色子：自旋为
整数倍（
）的粒子，波函数对于两个粒子交换总是对称的，例如
介子（
），光子（
）。它们遵守Bose统计，称为Bose子。
费米子：自旋为
半奇数倍（
）的粒子，波函数对于两个粒子交换总是反对称的，例如电子，质子，中子等。它们遵守Fermi 统计，称为Fermi子。
由“基本粒子”组成的复杂粒子，例如
粒子（氦核）或其它原子核，如在讨论的问题或过程中内部状态保持不变，即内部自由度完全被冻结，则全同性概念仍然适用，也可以当成一类全同粒子来处理。如果它们是由Bose 子组成，则仍为Bose子。如它们由奇数个Fermi 子组成，则仍为Fermi子；但如由偶数个Fermi子组成，则构成Bose子。
（4）Pauli不相容原理：不容许有两个全同的Fermi子处于同一个单粒子态。
地址：安徽省芜湖市北京东路1号 邮编：241000 建议使用1024 x 768分辨率
版权所有：安徽师范大学物理与电子信息学院
）的共同本征函数
（三重态）