|
安徽师范大学 精品课程——量子力学
|
《量子力学》基础习题
1.在0K附近,钠的价电子能量约为3电子伏,求其德布洛意波长。
2.氦原子的动能是![]() (k为玻耳兹曼常数),求
(k为玻耳兹曼常数),求![]() 时,氦原子的德布洛意波长。
时,氦原子的德布洛意波长。
3.设质量为![]() 的粒子在谐振子势
的粒子在谐振子势![]() 中运动,用量子化条件求粒子能量E的可能取值。
中运动,用量子化条件求粒子能量E的可能取值。
4.两个光子在一定条件下可发转化为正负电子对。如果两光子的能量相等,问要实现这种转化,光子的波长最大是多少?
5.证明在定态中,几率密度和几率流密度与时间无关。
6.由下列两定态波函数计算几率流密度;
(1)![]() , (2)
, (2)![]()
7.求粒子在一维无限深势阱 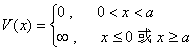 中运动的能级和波函数。
中运动的能级和波函数。
8.证明(2.6-14)式中的归一化常数是![]() 。
。
9.求一维线性谐振子处于第一激发态时几率最大的位置。
10.一维运动的粒子处于如下状态:
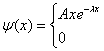
![]() 其中
其中![]() ,
,
(1)
将此波函数归一化,
(2)
问在何处找到粒子的几率最大?
11.设在球坐标系中,粒子的波函数为![]() ,
,
求 (1)在球壳![]() 中找到粒子的几率,
中找到粒子的几率,
(2)在![]() 方向,立体角元
方向,立体角元![]() 中找到粒子的几率。
中找到粒子的几率。
12. 求三维各向同性谐掁子![]() 的能级和波函数。
的能级和波函数。
13.设![]() 和
和![]() 都是一维定态薛定谔方程的解,而且它们属于同一能级E,试证明:
都是一维定态薛定谔方程的解,而且它们属于同一能级E,试证明:
![]() constant.
constant.
14.上题中,若![]() 和
和![]() 描述的都是束缚态,试证明
描述的都是束缚态,试证明![]() 和
和![]() 只相差一个常数因子。(提示:所谓束缚态,即当
只相差一个常数因子。(提示:所谓束缚态,即当![]() 时有
时有![]() )
)
15.一维线性谐振子处于基态![]() ,求
,求
(1)势能的平均值![]()
(2)动能的平均值![]()
(3)动量的几率分布函数。
16.氢原子处于基态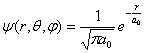 ,求:
,求:
(1)![]() 的平均值;
的平均值;
(2)势能![]() 的平均值;
的平均值;
(3)最可几半径;
(4)动能的平均值;
(5)动量的几率分布函数。
17.一刚性转子转动惯量为I,它的能量的经典表示式是![]() 。L为角动量。求与此对应的量子体系在下列情况下的定态能量及波函数:
。L为角动量。求与此对应的量子体系在下列情况下的定态能量及波函数:
(1)转子绕一固定轴转动;
(2)转子绕一固定点转动。
18.一维运动的粒子的状态是
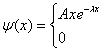
![]() 其中
其中![]() ,求
,求
(1)粒子动量的几率分布函数;
(2)粒子的平均动量。
19.在一维无限深势阱中运动的粒子,势阱的宽度为![]() ,如果粒子的状态由波函数
,如果粒子的状态由波函数![]() 描写,A为归一化常数,求粒子能量的几率分布和能量的平均值。
描写,A为归一化常数,求粒子能量的几率分布和能量的平均值。
20.设氢原子处于状态
![]()
求氢原子的能量,角动量平方及角动量z分量的可能值,这些可能值出现的几率和这些力学量的平均值。
21.求(3.7)题中粒子位置和动量的测不准关系![]()
![]()
22.已知![]() 和
和![]() 是二个厄密算符,试证明:
是二个厄密算符,试证明:
(1)
![]() 也是厄密算符
也是厄密算符
(2)
![]() 也是厄密算符
也是厄密算符
23.求解算符![]() 的本征值和本征函数。
的本征值和本征函数。
24.令![]() 和
和![]() ,试证明
,试证明
(1)
![]() ,(2)
,(2)
![]()
25.求动量表象中角动量![]() 的矩阵元和
的矩阵元和![]() 的矩阵元。
的矩阵元。
26.求一维无限深势阱中粒子的坐标和动量在能量表象中的矩阵元。
27.求在动量表象中线性谐振子的能量本征函数。
28.求线性谐振子哈密顿量在动量表象中的矩阵元。
29.设已知在![]() 和
和![]() 表象中,算符
表象中,算符![]() 和
和![]() 和矩阵分别为
和矩阵分别为
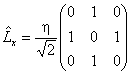 ,
, 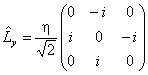
求它们的本征值和归一化的本征函数。最后将矩阵![]() 和
和![]() 对角化。
对角化。
30.求下面四个矩阵元:![]() ,
,![]() ,
,![]() 和
和![]() 。
。
31.已知某表象的三个基矢为:![]() ,有两个算符
,有两个算符![]() 和
和![]() ,它们有如下性质:
,它们有如下性质:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
试写出算符![]() ,
,![]() ,
,![]() 和
和![]() 的矩阵。
的矩阵。
32.实际原子核不是一个点电荷,它具有一定大小,可近似视为半径为![]() 的均匀分
的均匀分
球体它产生的电势为
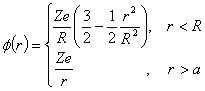
![]() 为核电荷,试把非点电荷效应看成微扰,
为核电荷,试把非点电荷效应看成微扰,
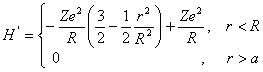
计算原子的![]() 能级的一级微扰修正。
能级的一级微扰修正。
33.设![]() ,
,
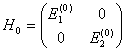 ,
,![]() (
(![]() 为实数)
为实数)
用微扰论求解能级修正(准到二级近似),并与严格解(把![]() 矩阵对角化)比较。
矩阵对角化)比较。
34.一维无限深势阱(0,a)中的一个粒子在![]() 时刻处于如态:
时刻处于如态:
![]() ,
,
求![]() 时刻的状态波函数。
时刻的状态波函数。
35.已知某体系的哈密顿算符![]() ,其中无微扰哈密顿算符
,其中无微扰哈密顿算符![]() 和微扰
和微扰![]() 在
在![]() 表象中的矩阵分别为:
表象中的矩阵分别为:
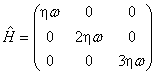 ,
, 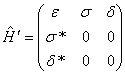 ,
,
试用微扰论方法求能级。(精确到二级修正)
36.体系无微扰的能级E是二度简并,波函数是![]() 和
和![]() ,它们是相互正交归一的。现有微扰
,它们是相互正交归一的。现有微扰![]() ,而且有
,而且有![]() ,
,![]() ,
,
求一级近似的能级和相应的零级近似波函数。
37.求证:![]()
38.在![]() 本征态
本征态![]() 下,求
下,求![]()
![]()
39.在![]() 表象中,求
表象中,求![]() 和
和![]() 的本征值和本征矢量。
的本征值和本征矢量。
40.求自旋角动量在![]() 方向的投影
方向的投影
![]()
的本征值和所属的本征函数。
41.设氢原子状态是
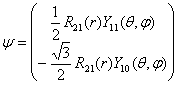
(1)求轨道角动量z分量![]() 和自旋角动量z分量
和自旋角动量z分量![]() 的平均值;
的平均值;
(2)求总磁矩 ![]() (SI)
(SI)
的z分量的平均值(用玻尔磁子表示)。
42.一体系由三个全同的玻色子组成,玻色子之间无相互作用。玻色子只有两个可能的单粒子态。问体系可能的状态有几个?它们的波函数怎样用单粒子波函数构成?
43.证明![]() ,
,![]() ,
,![]() 和
和![]() 组成正交归一系。
组成正交归一系。
44.设两电子在弹性中心力场中运动,每个电子的势能是![]() 。如果电子之间的库仑能和
。如果电子之间的库仑能和![]() 可以忽略,求当一个电子处在基态,另一个电子处于沿x方向运动的第一激发态时,两电子组成体系的波函数。
可以忽略,求当一个电子处在基态,另一个电子处于沿x方向运动的第一激发态时,两电子组成体系的波函数。
地址:安徽省芜湖市北京东路1号 邮编:241000 建议使用1024 x 768分辨率
版权所有:安徽师范大学物理与电子信息学院